www.mathematik-verstehen.de© Prof. Dr. Dörte Haftendorn
http://haftendorn.uni-lueneburg.de/mathe-lehramt/geschichte/stochastik/stochastik.htm
[Stochastik]  [Numerik]  [Computer]  [MuPAD] 

Regression


Beschreibende Statistik, Methode der kleinsten Quadrate
Beweise zur Regression

Gegeben sind Stützpunkte mit .

Zu jeder Geraden lassen sich mit

die "Ordinatenfehler", die

Residuen bilden. Gesucht ist die Gerade, für die die Summe der Quadrate der Ordinatenfehler minimal wird.

In Bild 2 ist eine beliebige Gerade mit zugehörigen Fehlerquadraten eingezeichnet.

  • Zwei-Variablen-Statistik, Regressionen   Handzettel   im Webplayer     download  

    • Darin ist auch eine frei bewegliche Gerade vorgesehen mit Anzeige der Fehlerquadratsumme.
  • Alle Formeln zu Ausgleichsgeraden und anderen Ausgleichskurven (Seiten 11 a und 11 b)

    • Aufstellen einer von m und b abhängigen Funktion



    Mit der Bezeichnung f(m,k)ist diese Fehlerquadratsumme in dem (oberen) GeoGebra-Bild als Rechteck bei C dargestellt. Es ist dort auch der Wert als Zahl sichtbar.
    Die darunter gezeigte Eukliddatei zeigt den Wert als Termwert an.



    Eine Gerade, dagestellt mit ihrer Fehlerquadratsumme in GeoGebra
        interaktiv


    Interaktive Seite mit Euklid         
    Wie findet man nun die Steigung m und den Achsenabschnitt b (oder k) so, dass die Fehlerquadratsumme minimal wird?
    Mit GeoGebra ist mir eine superschöne interaktive Version gelungen, die m und k sichtbar und auch zahlenmäßig liefert.
    Sie beruht auf folgender Idee:
    Die Fehlerquadratsumme f(m,k) ( oben q(m,b)) ist eine Parabel, wenn man k als x und m als Parameter auffasst.
    Ebenso ist sie eine Parabel, wenn man m als x und k als Parameter auffasst.
    Diese beiden Parabeln sind in den folgenden Bildern dünn in blaugrün gezeichnet.
    Ihre Scheitel sind mit A und B bezeichnet.
    Variiert man nun m, bewegt sich die erste Parabel und der Scheitel A hat eine Ortskurve, die auch eine Parabel ist. Sie wird beim von GeoGebra dick rot gezeichnet. Ebenso ist die Bahn von B dick lila, wenn k variiert wird. Man kann diese Parabeln als Schnitte des Paraboloids f(m,k) (bzw. q(m,b) auffassen.
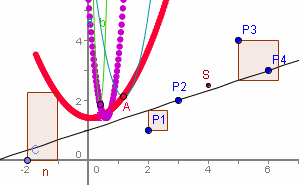
  • Methode der kleinsten Quadrate in superschöner interaktiver Darstellung AUSRUFEZ.GIF 32x32
    •    

    Die minimale Fehlerquadratsumme hat man ersichtlich dann, wenn sowohl A als auch B ihre tiefste möglich Lage einnehmen.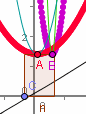
    In der tiefsten Lage von A und B sich die Ordinaten von A und B gleich der minimalen Fehlerquadratsumme.
    Ausgleichsgeraden und Ausgleichskurven aller Art
  • Regression, Ausgleichskurven Fitgeraden, Regressionsgerden
  • Alle Formeln zu Ausgleichsgeraden und anderen Ausgleichskurven (Seiten 11 a und 11 b)
  • Kovarianz, Korrelationskoeffizientimg    
    		•

    Beweis mit Methoden der Analysis

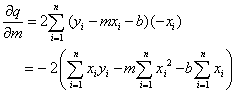
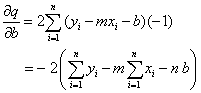
    Beide partiellen Ableitungen müssen Null sein. Also aus der Ableitung nach b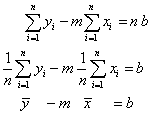

    Man sieht hier, dass die gesuchte Gerade durch den Schwerpunkt der Daten verlaufen muss, letzter ist rechts rot eingezeichnet.img/image114.gif 266x96

    In die Ableitung nach m eingesetzt ergibt sich
    und damit

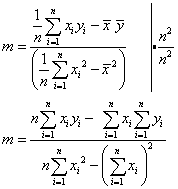
    In diesem Beispiel ist m=0,6 und b=0,1 die Gerade also y=0,6 x + 0,1


    Übrigens ist damit auch

     
    [Stochastik]  [Numerik]  [Computer]  [MuPAD] 
    Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Apr. 2002, update 30.10.2013
    www.mathematik-verstehen.de         www.doerte-haftendorn.de
    http://haftendorn.uni-lueneburg.de     http://mathematik.uni-lueneburg.de