Numerik Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/numerik/numerik.htm       © Prof. Dr. Dörte Haftendorn

Download des MuPAD-Notebooks (140 KB)     Save Link Taget As..., Verküpfung speichern unter... Periodische Kommazahlen
Mathematik mit MuPAD: Prof. Dr. Dörte Haftendorn, Mai 2004

• DIGITS:=40   //Dezimalen-Anzeige vergrößern

• float(1/17)

So kann man die Periodenlänge ablesen.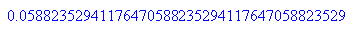
Experimentiere mit 1/n , wie lang ist jeweils die Periode?

• n:=13: [1/n,float(1/n)]

Versuche abbbrechende und nicht abbrechende Kommazahlen zu sortieren.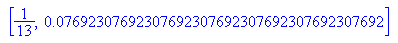
Bei welchen Nennern n bricht die Kommazahl 1/n ab?

• n:=2^3*5^7: [1/n,float(1/n)]

• //--------------------------------------------------------

Experimentiere: bei welchen Nennern n erhält man echte Vorperioden?
Vorperioden sind hinter dem Komma Ziffern ungleich Null, die nicht in der Periode vorkommen

• n:=16*17: [1/n,float(1/n)]

• //-------------------------------------------------------

Rückverwandlung von periodischen Kommazahlen in Brüche

• DIGITS:=8:

• [1/(10^n-1),float(1/(10^n-1))] $n=1..5

• [23/(10^n-1),float(23/(10^n-1))] $n=2..5

• [2347/(10^n-1),float(2347/(10^n-1))] $n=4..7

Also erzeugen die Nenner mit lauter Neunen Perioden, die genau dem Zähler entsprechen, aufgefüllt mit Nullen.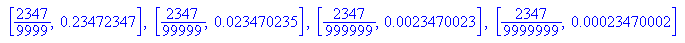
Die Periodenlänge ist gleich der Anzahl der Neunen.
Umgekehrt: Für die Rückverwandlung sofort-periodischer Dezimalzahlen muss man offenbar die
Periode als Zähler nehmen und als Nenner soviele Neunen wie die Periodenlänge angibt.

• DIGITS:=40:

• [0.123456712345671234567,1234567/9999999,float(1234567/9999999)]

Kommazahlen mit Vorperiode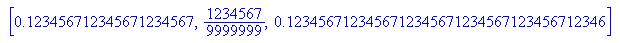
Man muss den Vorperiodenteil abtrennen.

• [0.345123456712345671234567,345,"+",1234567/9999999];
  [345+1234567/9999999000,float(345+1234567/9999999)/1000]

• float(0.345+1234567/9999999000)

Mit dem Befehl des CAS bekommt man nur Näherungslösungen: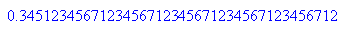

• numeric::rationalize(0.34512345671234567)
  

• float(%)

• 588235294117647/9999999999999999

• //------------------------------------------------------

Die Periodenlänge teilt Phi(n)=Euler(n), wenn N teilerfremnd zu 10 ist.
Bestätigen Sie das für etliche Beispiele.
Beschaffung von EulerPhi

• numlib::phi(3*11*13)

• n:=3*11*13: [1/n,float(1/n)]

Periodenlänge 6 und 6 teilt tatsächlich 240.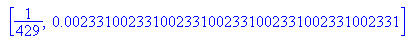

Experimentierfeld:

• float(1/137)

• float(1/(2*137));float(1/(16*137));

• float(1/17);float(1/(16*17));

• float(1/11);float(1/(4*11));float(1/(44*11));

• numlib::phi(44)

• DIGITS:=52

• float(1/3);float(1/(4*3));float(1/(7*17));

• 6*16
  

• float(1/(11*11));float(1/(7*19));float(1/(11*17));

• numlib::phi(121)

• float(1/(16*11));float(1/(4*3));float(1/(256*17));

• float(1/256)

• float(1/4);float(1/44)

• float(1/4);float(1/(4*17));float(1/17);float(1/34)

• float(1/29);float(1/(4*29));float(1/(16*29));float(1/(3125*29))

• 1/5^5;float(%)

• 1/99;float(%)

• 34*78

• 2652/9900

• float(221/825)

[Numerik]   Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Mai. 2004, update 14. August 2011

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]     [haftendorn.uni-lueneburg.de/ing-math]