Chaos und Fraktale
|
Johanneum Lüneburg | Dr. Dörte Haftendorn Chaos und Fraktale |
|
|
| Informationssystem | ||||
| Mathematik Chaos |
 Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten |
Lorenz-Attraktor
Der Meteorologe Edward Lorenz wollte mit seinem
Differentialgleichungssystem eine Wetterentwicklung beschreiben. Hier und auch in vielen
anderen "dynamischen Systemen" wird eigentlich das Verhalten im
"Phasenraum" beschrieben. Die Koordinatenachsen des Phasenraumes bedeuten dann
physikalische Größen, wie Druck, Temperatur,....
Die ersten Untersuchungen von Lorenz liegen schon vergleichsweise lange (nämlich 1961)
zurück. Seine Entdeckung war für die anderen Meteorologen zu mathematisch, und die
Mathematiker lasen keine meteorologischen Fachzeitschriften. Erst als in den achtziger
Jahren die Kenntnis chaotischer Zusammenhänge wuchs, kam seine Entdeckung zu Ehren.
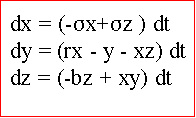Man betrachtetet das Differentialgleichungssystem:
Sigma, r und b sind Parameter, die Form des Attraktors bestimmen.
Sigma=10, r=28 , b=8/3
Man startet mit t=0 an einem Raumpunkt P(x0,y0,z0)= (0.001, 0.001, 0.001), rechnet die
Koordinatenänderung dx, dy und dz aus und erhält den Nachbarpunkt.
So entsteht die Bahn, der Orbit, des Punktes P.
Sie ist räumlich, daher kann man sie nur erfassen, wenn man sie von mehreren Seiten
ansieht.
Die Bilder zeigen den Attraktor in drei räumlichen Ansichten. Im
2. und 3.Bild ist außerdem das Verhalten von benachbarten verschiedenfarbigen
Startpunkten dargestellt. Besonders bei der Entstehung kann man sehen, wie sich die Bahnen
der Nachbarpunkte auseinanderentwickeln. Insgesamt aber werden sie von der Grenzfigur
= Limesfigur = Attraktor eingefangen, und je länger man beobachtet, desto
dichter wird der Attraktor. In Wahrheit schneiden sich nie zwei verschiedene dieser
Bahnen, was ein Bildschirm aber nicht wiedergibt. Auch eine einzelne Bahn hat keine
Kreuzungspunkte
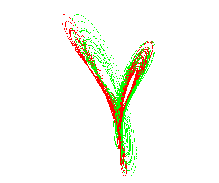Mit der letzten Graphik kann man den Lorenz-Attraktor räumlich sehen, wenn
man ihn mit einer rot-grünen Brille betrachtet.
Alle Bilder vom Lorenz-Attraktor wurden mit meinem Program Lorenz.pas © Ha94
erstellt.
| Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten |
Autor: © [Dr. Dörte Haftendorn] Datum Januar 98. Letzte Änderung am
[Fächer]
[Mathematik] [Chaos] [Webteam] [] 
zum Roessler-Attraktor