
Chaos und Fraktale
 |
Johanneum Lüneburg | Dr. Dörte Haftendorn Chaos und Fraktale |
||
| Informationssystem | ||||
| Mathematik Chaos Feigenbaum |
![]()
|
Logistische ParabelGrundlegende Erklärungen
|
 f
ist die Trägerfunktion für die rekursive Folge an.
f
ist die Trägerfunktion für die rekursive Folge an.
Die logistische Gleichung beschreibt viele Vorgänge in Natur und Technik. Insbesondere in der Biologie kann man an deuten als Bevölkerungszahl z.B. einer Mäusepopulation in einem begrenzten Lebensraum. Der Parameter r ist dann aus Geburten-und Sterberate zusammengesetzt, mit n ist die Zyklus-Zeit, etwa Wochen, gemeint. Die logistische Gleichung sagt dann aus, daß die Bevölkerungszahl proportional ist zum Produkt aus (momentaner) Bevölkerungszahl und “Abstand” von der Bevölkerungsgrenze.
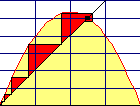
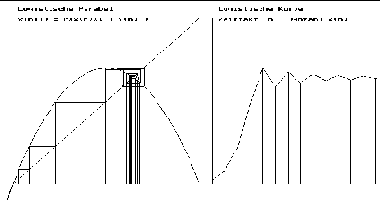
 Wie sich die Folge
verhält, wird rechts auf zwei Arten dargestellt. Links ist an
über an-1 aufgetragen. Man nennt
die Darstellung auch Spinnwebverfahren, Web-Darstellung,
Phasendiagramm.
Wie sich die Folge
verhält, wird rechts auf zwei Arten dargestellt. Links ist an
über an-1 aufgetragen. Man nennt
die Darstellung auch Spinnwebverfahren, Web-Darstellung,
Phasendiagramm.
Man startet bei beliebigem ao und zeichnet immer abwechselnd senkrecht zur Kurve und waagerecht zur Winkelhalbierenden.
Rechts sind die so zustandegekommenen Bevölkerungszahlen über der Zeit n aufgetragen.
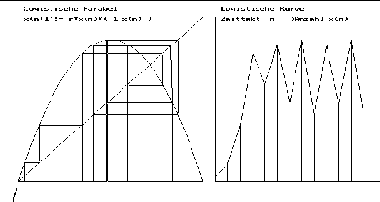
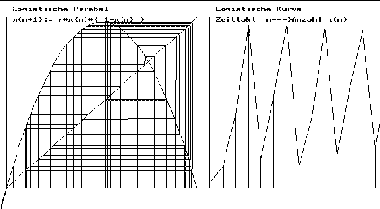 Das Verhalten der Folge wird im Wesentlichen von dem Parameter r
beeinflusst.
Das Verhalten der Folge wird im Wesentlichen von dem Parameter r
beeinflusst.
Für 0<r< 1 konvergiert die Folge gegen 0.
Für 1<r<3 konvergiert die Folge gegen den rechten Schnittpunkt mit der Winkelhalbierenden. Er ist dann anziehender Fixpunkt. Das ist er nämlich genau solange, wie die Steigung von f im Schnittpunkt betragsmäßig kleiner ist als 1. Für r<=1 schneidet die Parabel rechts nicht.
Für 3 < r treten zuerst mehrere Häufungspunkte auf, ab r=3,57 verhält sich die Folge chaotisch. Genauer und übersichtlich wird diese Abhängigkeit des Verhaltens vom Parameter r vom Feigenbaumdiagramm dargestellt.
Möglichkeiten mit dem Ti-92 |
|---|
| Leitseite |
|---|
![]()
![]() Autor: © [Dr. Dörte Haftendorn] Datum Januar 98. Letzte Änderung am 22. Jan. 99
Autor: © [Dr. Dörte Haftendorn] Datum Januar 98. Letzte Änderung am 22. Jan. 99
 [Fächer]
[Mathematik] [Chaos] [Feigenbaum] [Webteam] []
[Fächer]
[Mathematik] [Chaos] [Feigenbaum] [Webteam] [] 