
Chaos und Fraktale
 |
Johanneum Lüneburg | Dr. Dörte Haftendorn Chaos und Fraktale |
||
| Informationssystem | ||||
| Mathematik Chaos Feigenbaum |
![]()
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten |
|
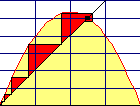
FeigenbaumdiagrammFeigenbaumszenario
|
| Das Feigenbaum-Szenario wurde von Mitchel Feigenbaum in den 70iger Jahren zuerst untersucht. Auf der Hochachse ist von oben nach unten der Parameter r für die logistische Gleichung in einem vorher gewählten Bereich aufgetragen. Die Rechtsachse hat x-Werte zwischen 0 und 1. Für jedes r aus dem Bereich entsteht eine Pixelzeile des Bildes. Es werden 100 Iterationen "im Dunkeln" gerechnet, für die nächsten 100 Iterationen wird ein Punkt in die Zeile gezeichnet. Wenn die Folge für dieses r konvergiert, sieht man nur das 200ste Pixel. Beim oberen Bild geht r von 2,9 (oben) bis 4 (unten). Bei r=3 tritt die erste Bifurkation auf. Man sieht für die nun folgenden r das 199ste und 200ste Pixel. Es liegen zwei Häufungswerte vor, bis r auf 3,449489... angewachsen ist. Diesen genauen Wert für r kann man aus den Schnitt- Steigungen der 2. Iterierten von f gewinnen. Es folgt eine Bifurkationskaskade, das Verhältnis der r-Abstände konvergiert gegen eine mathematische universelle Konstante, die Feigenbaum-Konstante =4,6692016091.... Der Eintritt ins Chaos erfolgt bei r=3,5699456... Das ist hier daran sichtbar, dass die Pixel von Nr. 101 bis 200 als breites Band sichtbar werden. In dem chaotischen Bereich gibt es aber immer wieder Inseln der Ruhe. In ihnen sind zunächst wieder wenige Häufungspunkte zu sehen. Deren Zahl ist nun aber keine reine Zweierpotenz mehr. Dann folgt wieder eine Bifurkationskaskade und erneuter Eintritt ins Chaos. | |
|---|---|
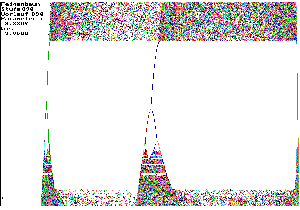 Fenster der Ruhe r = 3.82 bis r = 3.86 Dreierperiode großes Bild 39 K |
Feigenbaumdiagramm |
|
Möglichkeiten mit dem Ti-92 |
| Leitseite |
|---|
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten |
![]()
![]() Autor: © [Dr. Dörte Haftendorn] Datum Januar 98. Letzte Änderung am
Autor: © [Dr. Dörte Haftendorn] Datum Januar 98. Letzte Änderung am
 [Fächer]
[Mathematik] [Chaos] [Feigenbaum] [Webteam] []
[Fächer]
[Mathematik] [Chaos] [Feigenbaum] [Webteam] [] 