Informationssystemsystem Johanneum Lüneburg Dr. Dörte Haftendorn
Chaos und Fraktale		 Alphabetischer Index unten
Informationssystem
Mathematik  Chaos    

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Lindenmayer-Systeme, Wegfraktale

Grundlegendes

Realisierungen

nah Galerie der Wegfraktale

nahDimension

internZweigfraktal

internLOGO

internPascal

internL-System

nahTexte, Literatur, Links

nahBox-Dimension
nah Chaos-Seite

hoch hierhin Grundprinzip

Initiator ist meist ein gerader Strich, allgemein ein Linienelement.
Generator
Der Generator ist aufgebaut mit den Linienelementen des Initiators. Der Generator klärt, durch was der Initiator ersetzt werden soll. Am einfachsten geht es, wenn man den Generator aus geraden gleichlangen Stücken zusammensetzt.




Regel:
Jedes Linienelement (zunächst des Generators,dann in jeder Stufe) wird durch den verkleinerten Generator ersetzt. Das wird stets wiederholt.
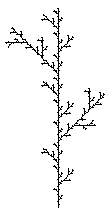
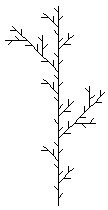
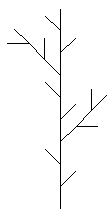
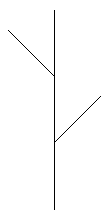
Zweig 4 Zweig 3 Zweig 2 Zweig 1

So entsteht stufenweise ein immer vielfältiger verzweigtes Bild. Dabei werden die kleinsten geraden Zweiglein immer kleiner. Bei diesem Zweig ist der Verkleinerungsfaktor 1/3. Dadurch gelangt man recht bald an die Grenzen der Darstellbarkeit. Das mathematische Fraktal ist die Grenzfigur dieses Prozesses. Man kann das Fraktal denken, sehen kann immer nur Vorstufen.
Stets wird beim Zeichnen ein Weg durchlaufen, deshalb habe ich diese Fraktale Wegfraktale genannt. In der einschlägigen Literatur wird meist nur "klassische Fraktale" (weil es sie schon länger gibt) gesagt, oder sie bekommen den Namen L-Systeme, nach Lindenmayer. Auch den Namen Graphtale habe ich schon gelesen.
Es sind vielfältige Variationen dieses Prinzips möglich, z.B. können zwei Generatoren im Wechsel oder in zufälliger Wahl wirken. Es könnten auch nur ein Teil des Linienelementes ersetzt werden u.v.m.
Der Kreativität werden (fast) keine Grenzen gesetzt.

Oben hoch hierhin Realisierung von Hand: Zumindest bei einigen im Karopapier realisierbaren Generatoren kann man drei bis vier Schritte ganz brauchbar zeichnen. Sicher sind solche Fraktale der erste Schritt im Unterricht.

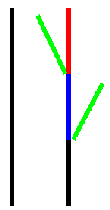
Realisierung mit rekursiven Prozeduren, z.B. in LOGO 

PR zweig :n :a

lokal "x"  lokal "y"    vi

     wenn :n=0 dann  vw :a rückkehr

     zweig :n-1 :a /3   re :wi

     setze "x"  xko  setze "y" yko

     zweig :n-1 :a /3    sprung :x :y   li :wi

     zweig :n-1 :a /3        li :wi

     setze "x"  xko  setze "y" yko

     zweig :n-1 :a /3    sprung :x :y    re :wi

     zweig :n-1 :a /3

ENDE

vw :a weist den "Igel" an, a Pixel vorwärts zu laufen. re :wi und li :wi sind Drehungen der Blickrichtung um die Gradzahl :wi. Im Befehl setze werden die momentanen Koordinaten gemerkt und bei sprung wieder angesprungen. Damit werden die Verzweigungsknoten realisiert. In der Arbeit mit nahLOGO habe ich einige Erfahrung. In diesem Thema ist LOGO außerordentlich geeignet.

Oben hoch hierhin Realisierung mit rekursiven Turtlegraphik-Prozeduren in Pascal
Eigentlich gibt es keine Turtlegraphik mehr in Pascal. Gerade wegen dieses Themas habe ich aber eine turtle-Unit geschrieben, die die mit der alten (Version kleiner 4) Pascalsyntax, die an das engliche LOGO angelehnt war, wieder verfügbar macht. Sie können diese und dasProgramm zweig.pas und zweig.exe © Ha94herunterladen.

Disk Beachten Sie unbedingt die Hinweise zum Laden meiner Pascalprogramme. Mit dem Programm zweig kann man etwa 20 Fraktale in jeder sinnvollen Stufe zeichnen.

Oben hoch hierhin Realisierung mit Lindenmayer-Systemen Ursprünglich wurden die L-Systeme 1968 von dem Biologen Aristid Lindenmayer zur Beschreibung des Pflanzenwachstums entwickelt.
Aus einem Axiom und einer oder mehreren Ersetzungsregeln wird zuerst entsprechend der gewählten Stufe ein langes Wort gebildet. Dessen Buchstaben werden dann einzeln gelesen und in Turtlegraphik-Befehle umgesetzt. Dabei steht F z.B: für fd(a), + für lt(b) , - für rt(b) bei einer Realsierung in Pascal, b.z.w. F z.B: für vw :a, + für li :b, - für re :b bei einer Realsierung in deutschem LOGO. In englischem LOGO steht fd statt vw, lt statt li und rt statt re. Die Klammern markieren die "Knoten", an denen die Zweige beginnen.

Mit diesem Prinzip sind auch die obigen JAVA-Applets erzeugt. Weiteres in der Galerie der Wegfraktale.

    Zweig-Fraktal

  1. Das Axiom F (Stufe 0).
  2. Die Ersetzungregel für F ist F ( + F ) - F ( - F ) + F (Stufe 1).
  3. In Stufe 2 ist dann F ( + F ) - F ( - F ) + F ( + F ( + F ) - F ( - F ) + F ) - F ( + F ) - F ( - F ) + F ( - F ( + F ) - F ( - F ) + F ) + F ( + F ) - F ( - F ) + F entstanden.
  4. Für Stufe 3 ist wieder jedes F mit der Ersetzungsregel zu ersetzen, u.s.w. .
Die Länge der Lindenmayerworte wächst immens schnell, hier etwa exponentiell mit Basis 5. Das bringt progammiertechnische Probleme, die ich aber in dem Programm linde.pas bzw. linde.exe © Ha94 gelöst habe.
Blatt Beachten Sie unbedingt die Hinweise zum Laden meiner Pascalprogramme. Mit dem Programm linde kann man ohne Programmierkenntnisse Fraktale in jeder sinnvollen Stufe zeichnen, kreativ Regeln variieren oder erfinden und schöne Kreationen speichern und laden.
Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten



obenAutor: © [Dr. Dörte Haftendorn]  Datum März 97. Letzte Änderung am 29. April 2007
Informationssystem [Fächer] [Mathematik] [Chaos] [Dimension] [Galerie] [Webteam] [] Schulentwicklung