	Johanneum Lüneburg	Dr. Dörte Haftendorn Chaos und Fraktale
	Informationssystem
	Mathematik Chaos Wegfraktale Galerie

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

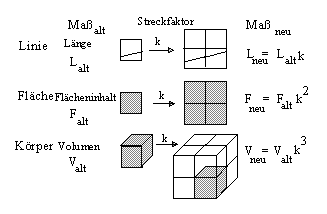Weiterführung dieser Themen nun im Bereich Mathe-lehramt an der Universität Lüneburg

Der Dimensionsbegriff

Stelle dir eine geometrische Figur vor und strecke sie dann mit dem Streckfaktor k.
Hast du die vorher die Länge L_alt gemessen, so hat deine Figur nachher die k-fache Länge.
Die rechte Abbildung zeigt dir, daß aber der Flächeninhalt k² -fach so groß wird, das Volumen wird sogar k³ -fach so groß.
Man sagt:

Eine Linie hat die Dimension 1.
Eine Fläche hat die Dimension 2.
Ein Körper hat die Dimension 3.
Ein Fraktal hat die Dimension dim.

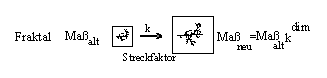
Wenn wir für Länge, Flächeninhalt, Volumen... als Maß bezeichnen, so gilt offenbar:

Maß _neu = Maß _alt k^dim

Fraktale haben nun die merkwürdige Eigenschaft, daß sie sich beim Strecken weder wie Linien, noch wie Flächen, noch wie Körper verhalten. Man muß bei ihnen zulassen, daß die Dimension nicht notwendigerweise ganze Zahl ist. Sie kann also eine Bruchzahl oder eine beliebige Kommazahl sein. Weil "fractum" (lat.) gebrochen, bzw. "fraction" (engl.) Bruch heißt, nennt man diese geometrischen Gebilde

Fraktale.

Auf der Seite Grundüberlegungen am Nikolaushaus wird das Obige nochmals am Beispiel nachvollzogen

Nicht genug, daß die Fraktale eine Erweiterung des Dimensionsbegriffes erfordern, es sind, je nach Art des oben genannten Maßes, auch noch verschiedene "Dimensionen" für ein Fraktal sinnvoll.

Wir werden die Selbstähnlichkeitsdimension d und die Boxdimension D genauer kennenlernen. Den Begründungen sind eigene Seiten gewidmet.

Die Zahlen d und D stimmen nicht immer überein. Bei selbstähnlichen Fraktalen, die sich nicht selbst überschneiden, gilt: d = D .

d bestimmt man durch Nachdenken über Bausteinzahl z und Streckfaktor k .

Dann rechnet man aus: Gleich2 . Nur bei selbstähnlichen Figuren ist die Berechnung von d sinnvoll.

D bestimmt man durch Messungen von Fraktalen, die mit verschiedenen Box-Gittern gerastert sind. Bei jeder geometrischen Figur, d.h. auch bei jedem Fraktal, kann man D wenigstens näherungsweise bestimmen..

Die Boxdimension ist vor allem für die Anwendung des Fraktalbegriffs in den Naturwissenschaften und der Medizin wichtig und sinnvoll.

Der Dimensionsbegriff	Grundüberlegungen	Leitseite Wegfraktale
Selbstähnlichkeits-Dimension	Box-Dimension	Messung der Boxdimension

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Autor: © [Dr. Dörte Haftendorn] Datum März 97. Letzte Änderung am 29. April 2007
[Fächer] [Mathematik] [Chaos] [Wegfraktale] [Galerie] [Webteam] []