	Johanneum Lüneburg	Dr. Dörte Haftendorn Chaos und Fraktale
	Informationssystem
	Mathematik Chaos Wegfraktale Galerie

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Selbstähnlichkeits-Dimension d

Ein Fraktal wird "streng selbstähnlich" genannt, wenn es aus gleichen Bausteinen besteht, die bei passender Vergrößerung genau wie das ganze Fraktal aussehen.

Leider kann man nie ein Fraktal genau zeichnen, sondern immer nur in "Stufen". Oft kann man ab der 3. Stufe schon sehen und überlegen wie es weitergeht, wenn die Stufenzahl immer mehr erhöht wird.
Die "Kochkurve" ist in dieser Hinsicht schön übersichtlich. z = 4 Bausteine

Wenn also z Bausteine das ganze Fraktal bilden und jeder Baustein, gestreckt mit dem Faktor k, ebenfalls das ganze Fraktal bildet, dann muß man ein Maß, das diese Abbildung "mitmacht", auf zweierlei Arten berechnen können:

Maß _neu = Maß _alt • z und Maß _neu = Maß _alt • k ^d
also Maß _alt • z = Maß _alt • k ^d
und es folgt

Dann ergibt sich .
Dabei kann log jeder Logarithmus sein.

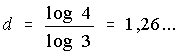Für die Kochkurve errechnet man nun: Selbstähnlichkeits-Dimension.
Suche in den folgenden Fraktalen passende Bausteine, rahme sie farbig ein.

Nicht alle diese Bilder sind streng selbstähnlich. In diesen Fällen ist die Dimensionsberechnung unsinnig.

Der Dimensionsbegriff	Grundüberlegungen	Leitseite Wegfraktale
Selbstähnlichkeits-Dimension	Box-Dimension	Messung der Boxdimension

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Autor: © [Dr. Dörte Haftendorn] Datum März 97. Letzte Änderung am 29. April 2007
[Fächer] [Mathematik] [Chaos] [Wegfraktale] [Galerie] [Webteam] []