Bäume

Diese schöne Bäume auf einer Seite

(Den Baum unten links auf der pdf-Seite sandte mir ein ehemaliger Schüler.)

Meine schönsten Bäume habe ich in Mathematica entworfen. Mit diesem Werkzeug kann ich in besonderer Weise meine fein differenzierten Wünsche umsetzen. Man hat Zugriff auf die Ausgangsstellung, das Schmalerwerden, die Winkel, die Verkürzung und die Farben. Für die Farbübergänge habe ich mir Funktionen entworfen, die in den unterstehenden Realisierung in der Funktion zweigFarbe verborgen sind.

Realisierung in Mathematica

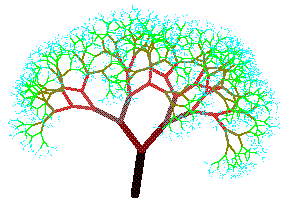
baumZF[stammVektor_,	zweigWinkelLinks_,stauchungLinks_,
			      	zweigWinkelRechts_,stauchungRechts_,
				stammDicke_,stauchungDicke_,
				iterationsTiefe_, options___]  :=
Module[{drehe,zweigZ, macheZweigeZ,alleZweigeZ},
	drehe[vec_,theta_]:={{Cos[theta],-Sin[theta]},{Sin[theta],Cos[theta]}}.vec;
	zweigZ[Line[{start_,ende_}]]:= {
	Line[{ende, ende+stauchungLinks
	drehe[ende-start,zweigWinkelLinks Random[Real,{0.5,1.5}]]}],
	Line[{ende,ende+stauchungRechts
	drehe[ende-start,zweigWinkelRechts Random[Real,{0.5,1.5}]]}] };
	zweigZ[Thickness[dicke_]] :=  Thickness [ stauchungDicke dicke] ;
	zweigZ[RGBColor[r_,g_,b_]] :=
		Module[ {},  zweigFarbe= RotateLeft[zweigFarbe];
		First[zweigFarbe]    ];
		macheZweigeZ[äste_]:=Flatten[ Map[ zweigZ,äste]];
	alleZweigeZ=NestList[ macheZweigeZ,{
		Thickness[ stammDicke], First[zweigFarbe],
		 Line[{{0,0},stammVektor}]},iterationsTiefe];
	Show[Graphics[alleZweigeZ ], options, AspectRatio->Automatic,PlotRange->All]
	]

Mathematica-Datei auf Anfrage

Dimension

Die Baumfraktale sind zwar im weitesten Sinne selbstähnlich, aber nicht überschneidungsfrei, daher ist es nicht sinnvoll, die Selbstähnlichkeitsdimension auszurechnen. Ein besseres Werkzeug ist die Boxdimension, bezogen auf die Baumkrone [Dimension]

Fraktale Dimension

Galerie der Wegfraktale

Leitseite Wegfraktale

[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]

(1996)(2002) Apr. 2005, update 16. August 2011

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]