Bäume mit zwei dicken Ästen

Der Stamm hat zwei Äste, die wieder zwei Äste mit zwei Ästen haben und so weiter. Sie sehen also ein Baum-Fraktal. Das eigentliche Fraktal muß man sich in Fortführung des Konstruktionsprinzips denken.

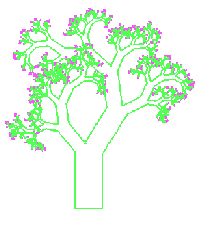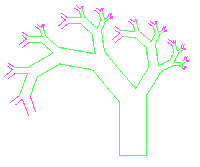
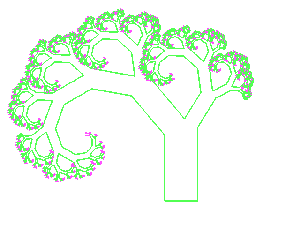
Oben sind die 2., 6. und 12. Stufe eines "strengen" Baumfraktals zu sehen. An ein offenes Astende wird stets ein dicker und ein dünner Ast gesetzt. Beim "strengen" Baum ist der dicke Ast stets links.
Nebenstehend ist mit fast demselben Pascalprogramm ein "Naturbaum" dadurch erzeugt, dass stets zufällig die linke oder die rechte Seite für den dicken Ast gewählt wird.

Realisierung in PASCAL

procedure Baum(i:integer;VAR gr,x,y,u,w:integer);
var xk,yk,uk,wk,g_l1,g_r1,g_lang,g_l:integer;
begin
  ..........
  if i=1 then begin
     setcolor(2);setlinestyle(0,0,3);
    zkn(i,x,y);fd(2*gr);zkn(i,u,w);fd(g_lang);
    setcolor(5);setlinestyle(0,0,3);
  end
  else begin
      fd(g_lang);kn(i,xk,yk);rt(50);pu;
      fd(g_r1);pd;kn(i,uk,wk);lt(90);
      zkn(i,xk,yk);
      Baum(i-1,g_r1,xk,yk,uk,wk);
      zkn(i,uk,wk);
      rt(162);kn(i,xk,yk);pu; fd(g_l1);pd;
      kn(i,uk,wk);lt(90);zkn(i,xk,yk);
      Baum(i-1,g_l1,xk,yk,uk,wk);
      zkn(i,uk,wk);
      rt(148);fd(2*gr);lt(180);
    end;
 .......

Dieses ist ein Stück us dem Programm zweig.pas.
Die Benutzung von Turtle-Graphik-Befehlen in Pascal wird auf der Leitseite "Wegfraktale" erläutert.
fd(30) heißt vorwärts 30 Pixel, lt(90) heißt 90° links wenden usw.
Mit kn werden die Koordinaten der Verzweigungsknoten gemerkt, mit zkn wird dahin zurückgesprungen.
Das Programm habe ich etwa 1990 geschrieben, heute würde ich es evt. anders machen. Grundsätzlich ist Pascal aber schwerfälliger als Logo.

Dimension

Die Baumfraktale sind zwar im weitesten Sinne selbstähnlich, aber nicht überschneidungsfrei, daher ist es nicht sinnvoll, die Selbstähnlichkeitsdimension auszurechnen.

Fraktale Dimension

Galerie der Wegfraktale

Leitseite Wegfraktale

[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]

(1996)(2002) Apr. 2005, update 16. August 2011

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]