haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm
haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm |
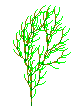 Wedel WedelGrößerer Wedel farbig 9 K (Logo) sw 7 K farbiger Wedel 13 K(Pascal) |
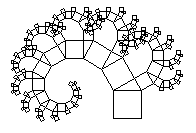 Pythagoras in größerem Bild 7 K |
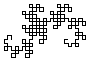
Drachenkurve Sie wäre eine Extraseite wert. Schön ist der Zusammenhang mit dem Papierfalten. |
PR wedel :n :a setze "r" 1/2 setze "wi" 22 lokal "x" lokal "y" wenn :n=0 dann vw :a rk farbe 0 128 0 wedel :n-1 :a*:r farbe 128 255 0 wedel :n-1 :a*:r setze "x" xko setze "y" yko li :wi wedel :n-1 :a*:r re :wi wedel :n-1 :a*:r farbe 0 255 0 re :wi wedel :n-1 :a*:r sprung :x :y re :wi wedel :n-1 :a*:r li :wi wedel :n-1 :a*:r li :wi wedel :n-1 :a*:r sprung :x :y ENDE |
PR pyth2 :länge quadrat :länge WENN :länge <4 DANN ( RE 90 VW :länge RK) VW :länge LI 30 pyth2 :länge * COS 30 pyth2 :länge * SIN 30 RE 30 VW :länge LI 90 ENDE PR quadrat :länge wh 4 [ vw :länge re 90 ] ENDE |
Zur Messung der Boxdimension sind Rasterbilder verfügbar |
 Kraut Kraut |
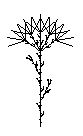 Dolde Doldein Variationen Meine schönste Dolde farbig 9K |
 |
Kraut 5 70 23 PR kraut :n :a :wi setze "r" 1/2 lokal "x" lokal "y" wenn :n=0 dann rk vw :a*:r setze "x" xko setze "y" yko li :wi kraut :n-1 :a*:r :wi re :wi sprung :x :y vw :a*:r setze "x" xko setze "y" yko re :wi kraut :n-1 :a*:r :wi li :wi sprung :x :y setze "x" xko setze "y" yko kraut :n-1 :a*:r :wi ENDE |
PR dolde :n :a setze "r" 1/2 setze "wi" 27 lokal "x" lokal "y" wenn :n=0 dann vw :a rk wenn (rest :n 2 )=0 dann ( zweig :n :a*:r*:r) sonst dolde :n-1 :a*:r setze "x" xko setze "y" yko li :wi dolde :n-1 :a*:r sprung :x :y re :wi dolde :n-1 :a*:r sprung :x :y re :wi dolde :n-1 :a*:r sprung :x :y li :wi ENDE |
PR dolde2 :n :a setze "r" 1/2 setze "wi" 27 lokal "x" lokal "y" wenn :n=0 dann ( vw :a rk) zweig :n-1 :a*:r*:r setze "x" xko setze "y" yko li :wi dolde2 :n-1 :a*:r sprung :x :y re :wi dolde2 :n-1 :a*:r sprung :x :y re :wi dolde2 :n-1 :a*:r sprung :x :y li :wi ENDE |
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] |