www.mathematik-verstehen.de
Link zum Buch
Site-Info[Geometrie] [Axiome] [Computer]
|
www.mathematik-verstehen.de |
| Link zum Buch Site-Info |
|
URL https://mathe.web.leuphana.de/geo/geoplus/axiome/axiome.htm [Geometrie] [Axiome] [Computer] | ||
| ||
 Axiome der Elementargeometrie |
 Dynamische Ergänzungen zum Buch: Mitschka, Strehl, Hollmann: Einführung in die Geometrie, div-Verlag 1998 (Hier wäre viel mehr möglich, wegen des fehlenden Bedarfs wurde das Projekt nicht fortgeführt) |
| V 1 Durch zwei verschiedene Punkten verläuft stets genau eine Gerade. |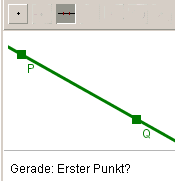 
|
Im jedem DGS gibt es ein Icon für "Punkt setzen". Weiter gibt es das Icon "Gerade zeichnen", das hier gerade aktiviert ist. Es wird gefragt nach dem "ersten Punkt", dann nach dem "zweiten Punkt", dann erscheint sofort die eine eindeutige Gerade. Wegen Axiom V 1 klappt das so. |
| V 2 Jede Gerade enthält mindestens zwei verschiedene Punkte. | Ohne zwei verschiedene Punkte schon zu haben, kann man das Werkzeug "Gerade zeichnen" nicht verwenden. Das sagt gerade das Axiom V 2. | |
| V 3 Es gibt mindestens drei verschieden Punkte, die nicht auf derselben Geraden. liegen. | 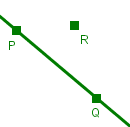 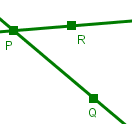 Diese beiden Bilder kann man zwar zeichnen, aber wenn gar nichts weiter kinzukommen darf, kann man damit nicht "euklidische Geometrie" betreiben. Es ist nämlich bei beiden Axiom V 1 nicht erfüllt. |
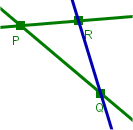 Hier sind alle drei Axiome erfüllt. Sie sehen ein "Modell" für das Axiomsystem V1, V2, V3. So richtig "Geometrie machen" können Sie sich damit zwar auch nicht vorstellen, es fehlen ja auch noch etliche Axiome der Euklidischen Geometrie. Aber man sieht: es muss bei einem DGS kein Icon für "Dreieck zeichnen" geben. Die Existenz von mindestens einem Dreieck ist schon durch V1, V2, V3 gesichert. |
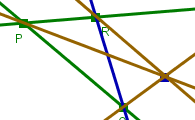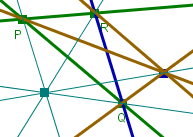  Jeder weitere Punkt außerhalb der bisherigen Geraden erfordert die Existenz weiterer Geraden. Naja, später ist die ganze Zeichenebene voller Punkte und Geraden, man kann dann die zeichnen, die man braucht. Vorläufig soll man sich aber vorstellen, dass es nicht mehr Objekte gibt als man sieht. |
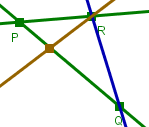 Dies ist auch ein "Modell" für das bisherige Axiomsystem. |
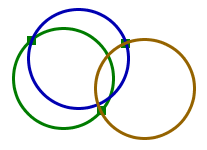 | In diesem "Modell" für das Axiom-System V1, V2, V3 gibt es 3 Punkte und 3 Geraden, sie sollen "Knopfgeraden" heißen. Von unserer höheren Warte aus sind die Knopfgeraden Kreise mit einheitlichem Radius. Immerhin, alle drei Axiome sind erfüllt. |
 www.mathematik-verstehen.de |
[Geometrie]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn Nov 2002, update |
Site-Info Link zum Buch |
| www.leuphana.de/matheomnibus www.doerte-haftendorn.de https://mathe.web.leuphana.de http://www.mathematik-sehen-und-verstehen.de |