Geometrie Leitseite URL
haftendorn.uni-lueneburg.de/mathe-lehramt/geo/geo.htm
[Mathematik der Griechen][Geometrie] [Goldener Schnitt] [Pentagon]     © Prof. Dr. Dörte Haftendorn
Goldenes Dreieck

Diese Seite druckgünstig in

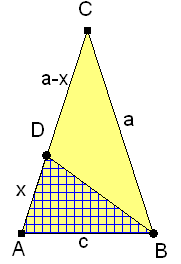Ein gleichschenkliges Dreieck mit den Basiswinkeln 72° heißt
"spitzes Goldenes Dreieck".
Teilt man bei ihm unten ein ebensolches Dreieck ab, bleibt ein
"stumpfes Goldenes Dreieck" mit den Basiswinkeln 36° übrig.

Es gilt:

Also teilt D den Schenkel des Goldenen Dreiecks im Goldenen Schnitt.


Erkundungsaufgaben:

Wie könnte man dieses Dreieck-Abteilen fortsetzen?

Gibt es eine Goldene Dreiecksschnecke?

Wo liegen besondere Punkte dieser Dreiecksfolge?

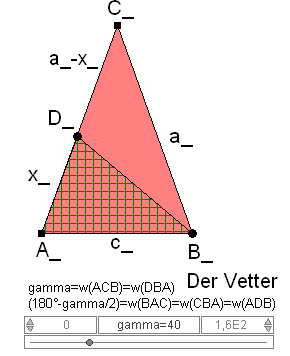Legt man den Winkel in der Spitze nach nicht fest, so erhält man einen "Vetter" des goldenen Dreiecks.

Hier gilt wie oben , was auch schon ganz hübsch ist.

Dann aber kommt man nicht weiter, weil zwar c=|DB| ist aber |DC| verschieden davon ist.


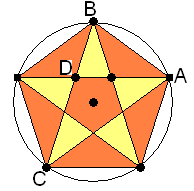Konstruktion: Die obigen Bilder sind mit dem Werkzeug: "Trage einen festen Winkel an" entstanden. Dadurch sind sie nicht "mit Zirkel und Lineal" konstruiert.

Ein solche echte Konstruktion könnte ausnutzen, dass das Goldene Dreieck im regelmäßigen Fünfeck oft auftaucht.

Dort sind die Mittelpunktswinkel 360°/5=72°, der Winkel ACB ist dazu der Umfangswinkel, der nach dem Umfangswinkelsatz 72°/2=36° groß ist. Also ist Dreieck ABC ein Goldenes Dreieck.

Damit ist nun durch das Obige schon bewiesen, dass sich die Diagonalen im regulären Fünfeck im Goldenen Schnitt teilen.

Weitere spitze Goldene Dreiecke sind die zu Dreieck BDA kongruenten und die kleinen gelben. Auch stumpfe goldene Dreiecke kommen reichlich vor. Wieviele Goldene Dreiecke sind es insgesamt?

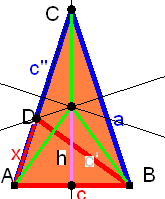Aus dieser Figur kann man die Seite c des regulären Fünfeckes aus dem Umkreisradius r =1 bestimmen:

h muss eliminiert werden. Gesucht ist c=Seitenlänge.

Es ergibt sich (mit Sorgfalt und etwas Mühe)

Dieses Ergebnis erhält man auch aus der Konstruktion der Pentagramm-Seite


Die Seitenlänge s des inneren Fünfecks ist bestimmt durch
Damit ist auch der Strauchfaktor vom großen auf das kleine Fünfeck bekannt, nämlich

[Mathematik der Griechen][Geometrie]  [Goldener Schnitt] [Pentagon]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Jan 2005, update 14. August 2011
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]