URLhaftendorn.uni-lueneburg.de/mathe-lehramt/kurven/transzendente/quadratrix/quadratrix.htm
[Geometrie]  [Mathematik der Griechen]  [Transzendente Kurven]  © Prof. Dr. Dörte Haftendorn

Quadratrix
und die Quadratur des Kreises
Druckversion mit Beweisen



Wie entsteht die Quadratrix?
Z wandert auf der y-Achse nach oben. Gleichzeitig dreht sich eine Ursprungsgerade. Wenn Z die Ordinate z hat, dann gilt für den Steigungswinkel
.
Man kann auch sagen Z und die Gerade bewegen sich gleichmäßig von der Nulllage so, dass sie gleichzeitig im Punkt (1/0) ankommen.
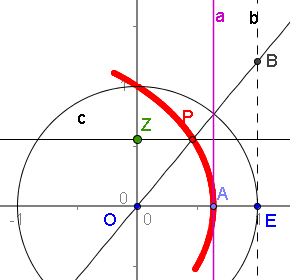Die Realisierung ist in Geogebra in gestuft aufgebaut.
Stufe 1 [ interaktiv]    [download] zeigt die Ortskurve von P. Dabei entsteht P als Schnitt der sich drehenden Geraden mit der Ordinatengeraden von Z.
Die oben genannte Formel zeigt, dass die Kurve trandzendent ist.		Stufe 2    [interaktiv]      [download]  entspricht diesem Bild.
In A, wo die Quadratrix die x-Achse schneidet, ist eine Senkrechte errichtet. Man kann A nicht mit Zirkel und Lineal konstruieren sondern nur "hinfummeln".
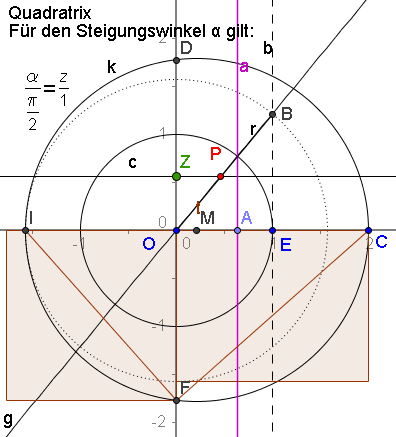Stufe 3  []    [] zeigt dann, wie die Kantenlänge eines Rechtecks erzeugt wird, dessen Flächeninhalt Pi ist.
Vorgehen: Die Senkrechte in A schneidet den Einheitskreis, die P erzeugende Gerade durch diesen Punkt schneidet die Tangente in E an den Einheitkreis in B. OB hat die Länge Pi/2. (Beweis )
Dann wird OB auf die y-Achse übertragen und ein Rechteck mit dieser Kante und der anderen Kante 2 gezeichnet.
Dieses Rechteck wird nun mit den üblichen Methoden in ein flächengleiches Quadrat verwandelt. Hier mit dem Thaleskreis, dem rechtwinkligen Dreieck IFC und dem Höhensatz. Der eine Hypothenusenabschnitt ist Pi/2, der andere 2, also ist das Höhenquadrat Pi.
Damit ist der Einheitskreis mit der Fläche Pi ein ein Quadrat der Fläche Pi verwandelt. "Der Kreis ist quadriert."
Wie schon unterwegs gesagt,s ist dieses aber keine "Konstruktion mit Zirkel und Lineal". Diese Näherungskonstruktion war aber schon den Griechen bekannt. (Quelle Schupp: Höhere Kurven)
[Geometrie]  [Mathematik der Griechen]  [Transzendente Kurven]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Dez. 2004, update 14. August 2011
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]