| Exponenten-Bereich in Excel |
download *.xls |
| Prof. Dr. Dörte Haftendorn |
Okt 02 |
|
| e |
10^e |
10^(-e) |
ed |
2^(ed) |
2^(-ed) |
|
| 50 |
1E+50 |
1E-50 |
1000 |
1,0715E+301 |
9,3326E-302 |
|
| 100 |
1E+100 |
1E-100 |
1001 |
2,143E+301 |
4,6663E-302 |
|
| 150 |
1E+150 |
1E-150 |
1002 |
4,286E+301 |
2,3332E-302 |
|
| 200 |
1E+200 |
1E-200 |
1003 |
8,5721E+301 |
1,1666E-302 |
|
| 250 |
1E+250 |
1E-250 |
1004 |
1,7144E+302 |
5,8329E-303 |
|
| 300 |
1E+300 |
1E-300 |
1005 |
3,4288E+302 |
2,9164E-303 |
|
| 350 |
#ZAHL! |
0 |
1006 |
6,8577E+302 |
1,4582E-303 |
|
| |
|
|
1007 |
1,3715E+303 |
7,2911E-304 |
|
| 300 |
1E+300 |
1E-300 |
1008 |
2,7431E+303 |
3,6456E-304 |
|
| 301 |
1E+301 |
1E-301 |
1009 |
5,4861E+303 |
1,8228E-304 |
|
| 302 |
1E+302 |
1E-302 |
1010 |
1,0972E+304 |
9,1139E-305 |
|
| 303 |
1E+303 |
1E-303 |
1011 |
2,1944E+304 |
4,557E-305 |
|
| 304 |
1E+304 |
1E-304 |
1012 |
4,3889E+304 |
2,2785E-305 |
|
| 305 |
1E+305 |
1E-305 |
1013 |
8,7778E+304 |
1,1392E-305 |
|
| 306 |
1E+306 |
1E-306 |
1014 |
1,7556E+305 |
5,6962E-306 |
|
| 307 |
1E+307 |
1E-307 |
1015 |
3,5111E+305 |
2,8481E-306 |
|
| 308 |
1E+308 |
0 |
1016 |
7,0222E+305 |
1,424E-306 |
|
| 309 |
#ZAHL! |
0 |
1017 |
1,4044E+306 |
7,1202E-307 |
|
| 310 |
#ZAHL! |
0 |
1018 |
2,8089E+306 |
3,5601E-307 |
|
| |
|
|
1019 |
5,6178E+306 |
1,7801E-307 |
|
| |
|
|
1020 |
1,1236E+307 |
8,9003E-308 |
|
| |
|
|
1021 |
2,2471E+307 |
4,4501E-308 |
|
| |
|
|
1022 |
4,4942E+307 |
2,2251E-308 |
|
| |
|
|
1023 |
8,9885E+307 |
0 |
|
| |
|
|
1024 |
#ZAHL! |
0 |
|
| |
|
|
1025 |
#ZAHL! |
0 |
|
| Zahl-Bereich in Excel |
 |
 |
 |
 |
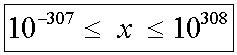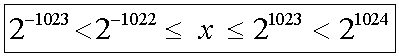| Vorzeichen 1 Bit
|
| Exponent 11 Bit, eigentlich 0 bis 2047,
|
| Von der so dargestellten Zahl wird 1023 abgezogen. |
| Damit werden auch negative Exponenten möglich. |
| Es folgen 13 Blöcke zu 4 Bit, d.h. 52 Bit, also 13 hexadez. Stellen.
|
| Die erste dieser hexadezimalen Stellen darf nicht 0 sein, das ist die 49. Stelle. |
| Daher ist 2^(-49) die Maschinengenauigkeit. |
| Zusammen sind das 64 Bit, also 8 Byte für eine Zahl in Excel, bzw. im Intel-Coprozessor.
|
Prof. Dr. Dörte Haftendorn 
LBS-Mathe] [Numerik] 
Genaueres zur Gleitpunktdarstellung nach IEEE-Standard siehe Extraseite.
[LBS-Mathe] [Numerik]