	Johanneum Lüneburg	Dr. Dörte Haftendorn Chaos und Fraktale
	Informationssystem
	Mathematik Chaos Wegfraktale Galerie

Bäume mit drei Ästen

Der Stamm hat drei Äste, die wieder drei Äste mit drei Ästen haben und so weiter. Sie sehen also ein Baum-Fraktal entstehen. Das eigentliche Fraktal muß man sich in Fortführung des Konstruktionsprinzips denken.

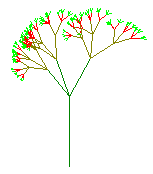
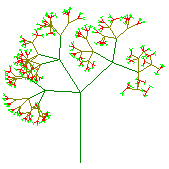
Oben sind die 5., 6. und 7. Stufe von Baumfraktalen zu sehen.

Realisierung in LOGO

PR baum :n :a :w
lokal "x" lokal "y" lokal "wi"
 wenn :n=0 dann farbe 0 255  0 vw :a rk
farbe 255/:n 150-150/:n  0
 vw :a
setze "x" xko setze "y" yko
setze "wi"  ( zz :w) + div :w 2
re :wi baum :n-1 5*:a/8 :wi punkt :x :y
li :wi
setze "wi"  ( zz :w)+ div :w 2 li :wi
baum :n-1 5*:a/9 :wi punkt :x :y re :wi
setze "wi"  ( zz :w)+ div :w 2   li 2*:wi
baum :n-1 4*:a/8 :wi  punkt :x :y re 2*:wi
ENDE

In der wenn- Zeile wird für die grünen Spitzen gesorgt.
Die Farben sind im RGB-System angegeben und von der Stufe n, bei der das entsprechende Aststück gezeichnet wird, abhängig.
Erklärung auf den Seiten Farben und Computer. Dann werden die Koordinaten der Verzweigungsknoten gemerkt. "wi" ist der Winkel, bei obigen Bildern 37°, in dem die die Äste abzweigen sollen. damit der Baum "natürlich" aussieht, ist hierfür eine kleine Zufallsschwankung (zz = Zufallszahl) vorgesehen.

Dimension

Die Baumfraktale sind zwar im weitesten Sinne selbstähnlich, aber nicht überschneidungsfrei, daher ist es nicht sinnvoll, die Selbstähnlichkeitsdimension auszurechnen.

Selbstähnlichkeitsdimension

Galerie der Wegfraktale

Leitseite Wegfraktale

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

Autor: © [Dr. Dörte Haftendorn] Datum März 97. Letzte Änderung am 29. April 2007
[Fächer] [Mathematik] [Chaos] [Wegfraktale] [Galerie] [Webteam] []