Drachen-Fraktal

Diese Seite als schönes DIN A4-Blatt als	Drachenfraktal in LOGO Dort auch Drachenfraktal als Lindenmayersystem. Drachen in mswLOGO Ziel Speichern unter.... öffnen mit mswLOGO Mehr zu mswLOGO
Die Drachenkurve entsteht durch fortgesetztes Papierfalten , wenn man einen langen Streifen Papier immer links über rechts faltet, dann jeden Knick rechtwinklig hinstellt und von oben betrachtet. Beim handwerklichen Falten verliert man schon bald die Übersicht, aber auf Karopapier kann man gewisse Gesetzmäßigkeiten entdecken.

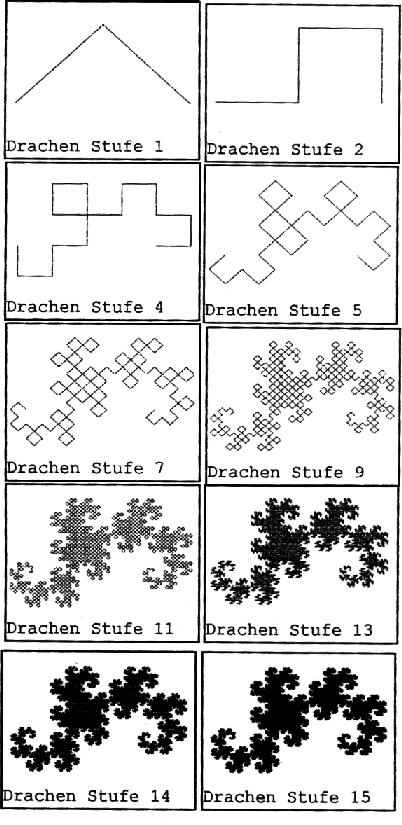
	Schreibt man Linksknicks als 1 und Rechtsknicks als 0, so ergeben sich nacheinander 0, 100, 1100100, 110110001100100, 101100111001000110110001100100 u.s.w., Zahlen, die man ganz leicht immer weiter schreiben kann. Die entstehenden Zahlen lassen sich als Dualzahlen interpretieren. Dann konvergieren Sie gegen die sogenannte Papierfaltungszahl. Manchmal wird die in Stufe 15 annähernd abgebildete Grenzfigur der Drachen genannt, ihr Rand ist dann die Drachenkurve.
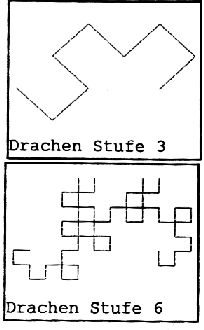
Man kann auch mit Varianten herumprobieren. Nimmt man Stufe 2 als Initiator und Stufe 3 als Generator, so erhält man den Zwillingsdrachen, dessen Rand eine Kochkurven-Variante mit dem Generator +F--FF++F- ist (+ = 45°). In dem Buch "Dino-Park" von Chrichton, das als "Jurassic Park" verfilmt worden ist, werden die Kapitel mit den Stufen des Drachenfraktals eingeleitet.

(1996)(2002) Apr. 2005, update 18. April 2012