Fraktale Geometrie Leitseite URL
haftendorn.uni-lueneburg.de/mathe-lehramt/fraktale/fraktale.htm
[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]   © Prof. Dr. Dörte Haftendorn

Fünfstern-Fraktal

Dies ist ein Fünfstern, an dessen Armen Fünfsterne sind, die an ihren Armen Fünfsterne tragen. Sie sehen also ein Fünfstern-Fraktal in 3. Stufe. Das eigentliche Fraktal muß man sich in Fortführung des Konstruktionsprinzips denken.
hoch ab Die drei Bilder unterscheiden sich noch in der Längenverkürzung von Stufe zu Stufe. Beim mittleren Fraktal ist der Stauchfaktor gerade so gewählt, dass das "wahre Fraktal" gerade noch überschneidungsfrei bleibt. (Schöne Anwendung von geometrischen Summen)

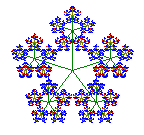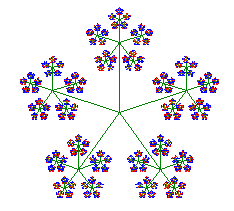
5Eckk4 5Eckk4 5Eckk4

hoch ab Das erste und das mittlere Fraktal in 4. Stufe.

5Eckk4 5Eckk4 Dieses Fraktal in Stufe 5
In Größe 300x300 8K
In Größe DIN A5 mit 14K

hoch ab Realisierung in LOGO

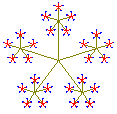
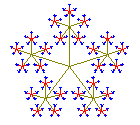
Mit q=3 ergibt sich das linke, mit q=2,618 =(3+Wurzel(5))/2 das mittlere Fraktal 
PR quintus :n :a
lokal "x" lokal "y"
;*q=2 ist zu groß q=3 ist zu klein q= 2,618 passt
setze "q" 2,618
wenn :n=0 dann farbe 0 0  255 quintusdann :a rk
   setze "x" xko setze "y" yko
      farbe 255/:n 150-150/:n  0
   vw :a quintus :n-1 :a/:q  punkt :x :y re 72
      farbe 255/:n 150-150/:n  0
   vw :a  quintus :n-1 :a/:q  punkt :x :y re 72
     farbe 255/:n 150-150/:n  0
  vw :a  quintus :n-1 :a/:q  punkt :x :y re 72
     farbe 255/:n 150-150/:n  0
  vw :a  quintus :n-1 :a/:q  punkt :x :y re 72
     farbe 255/:n 150-150/:n  0
  vw :a  quintus :n-1 :a/:q  punkt :x :y re 72
ENDE
Diese Prozedur quintusdann sorgt für den eigentlichen Fünfstern. Im nebenstehenden Fraktal-Hauptprogramm wird fünfmal das Fraktal von verkleinerter Stufe mit vrkürzten Längen aufgerufen. 
PR quintusdann :a
lokal "x" lokal "y"
setze "x" xko setze "y" yko
vw :a punkt :x :y re 72
vw :a punkt :x :y re 72
vw :a punkt :x :y re 72
vw :a punkt :x :y re 72
vw :a punkt :x :y re 72
ENDE

hoch ab Dimension

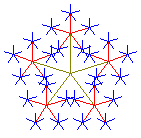
Das Fünfstern Fraktal ist selbstähnlich. Dabei vernachlässigt man eigentlich die inneren grünen Striche. Das linke und mittlere Fraktal sind überschneidungsfrei, hier lässt sich die Selbstähnlichkeitsdimension ausrechnen: d=log z / log q , also dlinks = log 5 / log 3 = 1,46 bzw. dmitte = log 5 / log 2,618 = 1,67. Dies bestätigt, das "flächige" Fraktale eine höherere Dimension haben als "filigrane".

nahSelbstähnlichkeitsdimension nahGalerie der Wegfraktale nahLeitseite Wegfraktale
[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1996)(2002) Apr. 2005, update 16. August 2011
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]