Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]    © Prof. Dr. Dörte Haftendorn

Der Höhenschnittpunkt wandert
auf paralleler Straße

Download als pdf- Arbeitsblatt(Ab Klasse 8)
Download als Word-97- Arbeitsblatt(Ab Klasse 8)


Prof. Dr. Dörte Haftendorn, Arbeitsblatt für Lehrer und Schüler ab Klasse 8 , T3-Tagung Wetzlar 2002

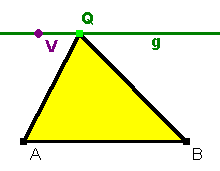
1) Konstruiere zur Strecke AB durch V eine Parallele g.

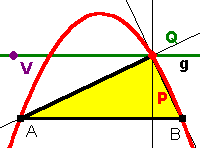
Setze den Punkt Q zugfest auf g
und färbe das Dreieck ABQ.

Speichere dieses Dreieck, denn es ist die Grundlage einer ganzen Aufgabenfamilie.

Probe: Wenn man an Q zieht wird das Dreieck nur geschert, g muss fest bleiben. Wenn man V bewegt, darf g nur parallel verschoben werden, hier also nur auf und ab parallel zu AB bewegt werden.

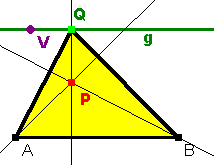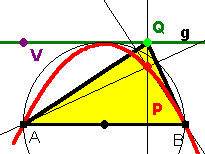
2) Konstruiere den Höhenschnittpunkt.

Prüfe, ob der Höhenschnittpunkt zugfest ist.

Wähle einen neuen Namen für diese Zeichnung und speichere sie.

Lasse Q auf der Straße g wandern und erzeuge die Ortslinie von P

Handwerk: Wähle das Icon "Ortslinie" und folge den Hinweisen in der Statuszeile.

Bei Dynageo(Euklid) erst P anklicken, dann Q ziehen.

Experimentieren, Beobachten und Nachdenken soll die Fragen klären helfen.
  • Frage A) Welche Ortslinienformen kommen vor?
  • Frage B) Welche besonderen Punkte liegen auf der Ortslinie?
  • Frage C) Welche Lage kann Q in Bezug auf die Ortslinie haben?
  • Frage D) Was ist Besonderes an dem Dreieck zu sehen, wenn die Ortslinie die Gerade g schneidet?

Lösungen

Halt, nicht vor dem Ausprobieren ansehen!!!!!!!!!!!!!!!!!!!!!!!!!!!

A)

  • Die Ortslinie ist ein Bogen.
  • Der Bogen könnte ein Parabelbogen sein.
  • Der Bogen kann unten nicht wieder zusammenlaufen, weil ja P immer auf der Höhe hc unter oder über Q liegt und Q auf der Geraden g ins Unendliche laufen kann. Also ist die Ortslinie kein Ellipsenbogen.
  • Der Bogen hat seinen Scheitel über der Mitte von AB.

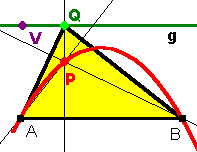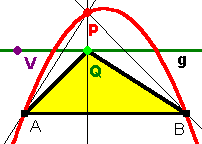
B) A und B müssen auf der Ortslinie liegen, denn wenn das Dreieck bei A bzw. B rechtwinklig ist, ist A bzw. B selbst der Höhenschnittpunkt P
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  (1998), Apr. 2002, update 02. Mai 2012
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]