Kreationen neuer Kurven durch Produktbildung

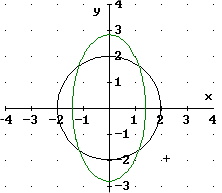Zwei Ellipsen in der Form und

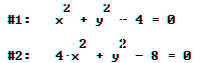haben die Graphen:

Das Produkt

muss als Graph genau die Vereinigung der beiden Graphen haben.

Dies ist dann eine algebraische Kurve 4. Grades, eine sogenannte Quartik.

Sehen wir uns die Raumfläche an:

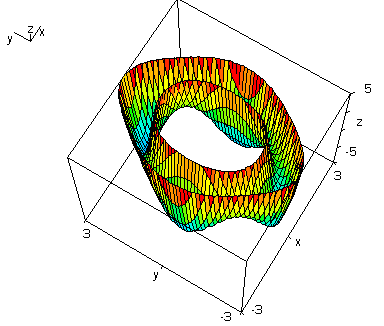
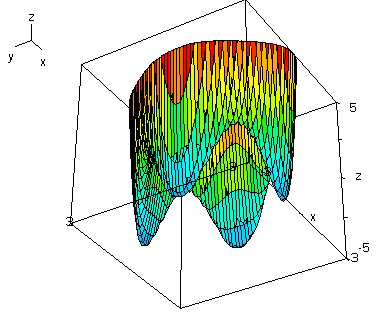
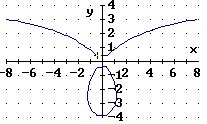
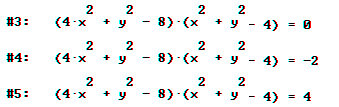Es wird klar, dass man diese Raumfläche auch in anderen Höhen als Null schneiden kann. Für die rechten Gleichungen liefert Derive die etwas "krüppeligen" Kurven

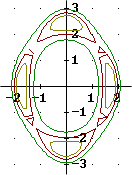Besonders schlecht ist #3, das oben exakt zu sehen ist.

Diese Quartiken aus Ellipsenprodukten hat schon Felix Klein untersucht. Mit unseren Möglichkeiten ist nun eine vollständige Beschreibung der möglichen Typen ganz einfach.

Durch Produktbildung öffnet sich ein ganzes Reich weiterer algebraischer Kurven.