Kurven und 3D-Raumflächen

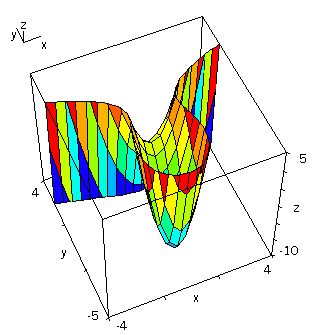Allgemein lässt sich jede algebraische Kurve schreiben als , wobei F ein Polynom n-ten Grades in x und y ist. Z.B. ist ein Polynom 5. Grades in x und y.

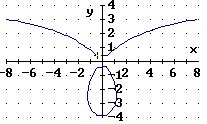
Die Strophoide mit der Gleichung ist also eine algebraische Kurve 3. Grades.

Hier gilt .

Nun ist aber mit eine Raumfläche beschrieben.

So ergibt sich die Strophoide als Schnittkurve dieser Raumfläche mit der Grundebene .

In Derive

und dann 3D-Graph

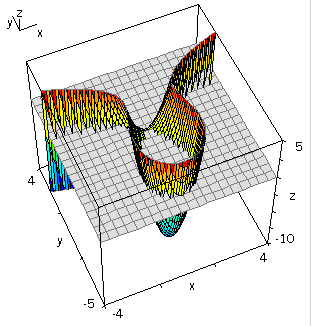Um die zackige Schnittlinie etwas zu unterdrücken, kann man das Gitter enger machen.

Auf dem Graph rechte Maustaste, Bearbeiten, 50 z.B.

Schöne Diskussion, warum kann der Computer das nicht besser? Wie macht der das eigentlich?

Nun sieht man, warum man 2D-Graphik mit

Folgendes erhält:

Jetzt ist aber auch klar, dass man mit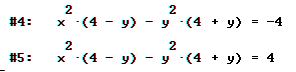
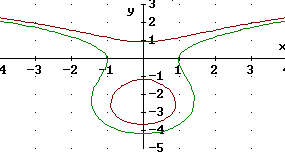Folgendes erwarten kann:

Dieses Vorgehen öffnet kreativer Arbeit Tür und Tor.

Datei kurven-3d.doc