Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] 
|
Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm
|
|
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] |
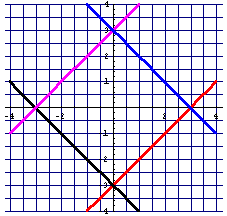
Hier siehst du ein Geradenkaro.
Auf der Geraden rechts oben liegen z.B. die Punkte
(-1/4), (0,3); (1,2), (2,1), (3,0), (4,-1),
die Summe aus x-Koordinate und y-Koordinate ist immer 3. Dafür schreibt man 
und nennt diese Gleichung die Gleichung der Geraden rechts oben.
Stelle die anderen Geradengleichungen auf.
Lösung:
lo:
lu:
ru:
ro:
Welche der folgenden Gleichungen sind auch richtig? Welche sind falsch?
a: 
b: 
c: 
d: 
e: 
f: 
Rechnerische Prüfung: Liegt der Punkt P(10/-13) auf der Geraden ro?
Antwort ja, denn 
ist wahr.
Liegt der Punkt P(10/13) auf der Geraden ro? Antwort nein, denn 
ist falsch.
Liegt der Punkt P(-3,7/6,7) auf der Geraden ro? Antwort ja, denn 
ist wahr.
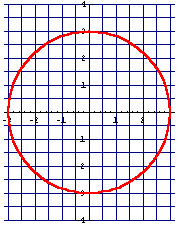Mathusalem hat einen Kreis um den Ursprung mit dem Radius 3.
Eine der folgenden Gleichungen soll die Gleichung dieses Kreises sein: a:
, b:
oder c:
Ganz sicher liegen die Punkte O(0/3), L(-3/0), U(0,-3), R(3/0) auf dem Kreis. Daher prüft Mathusalem mit diesen Punkten:
Prüfe O auf a?
,falsch, also ist a nicht die Kreisgleichung.
Prüfe O auf b?
,richtig, also kann b die Kreisgleichung sein. Prüfe R auf b? 
,richtig, also ist kann b immer noch Kreisgleichung sein. Man sagt auch: R erfüllt Gleichung b. Prüfe selbst L und U.
Mathix prüft R auf c? 
, wahr, also könnte auch c die Kreisgleichung sein.
Mathilde prüft O auf c? 
, falsch, also kann c doch nicht die Kreisgleichung sein. Da Mathusalem aber wusste, dass eine der Gleichungen a,b,c richtig ist, muss es b sein.
Man sagt: ist die Gleichung des Kreises um den Ursprung mit Radius 3 und der Kreis ist der Graph der Gleichung oder die Kurve zu der Kurvengleichung.
Gleichungen mit x und y und Kurven im x-y-Koordinatensystem entsprechen sich.
ist die Gleichung des "Rund-Ecken-Quadrats".
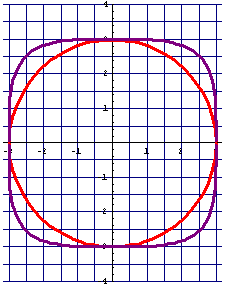
Prüfe, dass auch hier die Punkte O,L,U,R wahre Aussagen erzeugen.
Prüfe P(2,5/3,5) auf d? 
, streng genommen falsch, aber P ist nur ungefähr abgelesen, also kann man auch nur "ungefähr gleich" erwarten. Aber sicher ist: P erfüllt nicht b.
| Merke: Alle Punkte, deren Koordinaten aus der Kurvengleichung eine wahre Aussage machen, liegen auf der Kurve. Eine Gleichung, mit der ein sicher auf der Kurve liegender Punkt eine falsche Aussage erzeugt, ist sicher nicht die Kurvengleichung. |
| [Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] |
 Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn (1998), Apr. 2002, update |
| Direkte Internetadressen [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] |