Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm

[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] © Prof. Dr. Dörte Haftendorn

Kurven, Kurvengleichungen und Termumformungen

Download als pdf- Arbeitsblatt(Ab Klasse 8)
Download als Word-97- Arbeitsblatt(Ab Klasse 8)

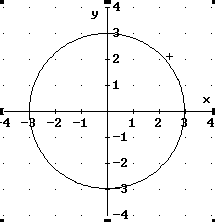
Gib in Derive in der Eingabezeile ein: x^2 + y^2 = 9 und

zeichne dazu den Graph. 2D-Graphikfenster, dort

Es ist der Kreis um den

Ursprung mit dem Radius 3.

Er hat die Gleichung , wie aus dem "Zusammenhang-Blatt" deutlich wurde.

Mit Derive kannst du zu allen dort angegebenen Gleichungen sofort die zugehören Kurven sehen. Probiere das aus.

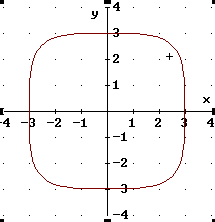
Dieses "Rund-Ecken-Quadrat" hat die Gleichung

REQ:
Prüfe, ob die folgenden Gleichungen richtige, erlaubte Umformungen dieser Gleichung sind. Stelle dazu die zu prüfende Gleichung zusammen mit dem Rund-Ecken-Quadrat REQ dar.

a: b: c:

d: e: f: g:

Welche der Kurven a bis g sind hier zusammen mit dem REQ dargestellt?

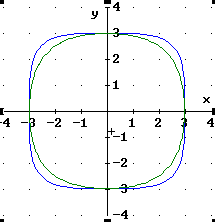
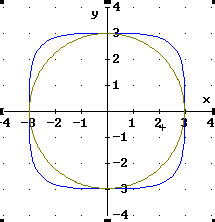
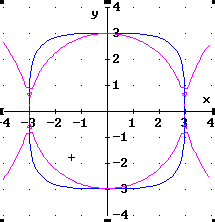
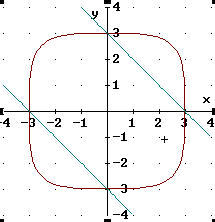
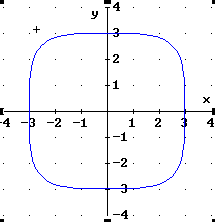
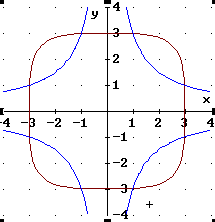
Was ist beim Umformen falsch gemacht?

Merke:
Wenn zu der umgeformten Gleichung eine andere Kurve erscheint, war die Umformung sicher falsch.
Erscheint dieselbe Kurve, kann die Umformung richtig sein.
Es kann aber auch sein, dass der Fehler so klein oder so geartet ist, dass man ihn am Computer nicht sieht.

[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn

(1998), Apr. 2002, update 02. Mai 2012

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]