Lehrerbildung zwischen Tradition und Innovation

 

Mathematik in Bewegung

 

'In Mathe war ich immer schlecht.' So bekommt man viel zu häufig -und oft gänzlich ungeniert- zu hören und der Mathematikunterricht genießt aus Sicht vieler Menschenkeinen sonderlich guten Ruf. Allerdings bezieht sich die Erfahrung ja auf vergangenen Mathematikunterricht, aber gerade im vergangenen Jahrzehnt kam die Schulmathematik in Bewegung.

Einen ersten heftigen Stoß vor den Bug bekam die Mathematiklehrerschaft 1995 durch die Habilitationsschrift von H. W. Heymann versetzt, der feststellte, dass auf die Breite gesehen vom Mathematikunterricht nach Klasse 7 weder nennenswert viel behalten noch gebraucht wird. Schlag auf Schlag zeigten die Untersuchungen TIMMS und PISA, dass wir uns wahrlich auf den mathematikbezogenen Schulerfolg nicht viel einbilden dürfen. Immer schon gab es auch die guten, beweglichen und an nachhaltigem Lernen interessierten Mathematik-Lehrenden. Viele von Ihnen hatten begonnen, die Chancen der aufkommenden Computer auszuloten und schon seit Beginn der neunziger Jahre versucht, eine veränderte Unterrichts- und Aufgabenkultur zu praktizieren. Die kalkülhafte Abarbeitung von Aufgaben konnte doch nicht mehr sinnvoll sein, wenn man - wie vielfach ausprobiert worden ist - die Aufgaben eines bayerischen Mathematikabiturs mit Computerwerkzeug in 10 Minuten löst. Leider haben die innovativen Lehrenden nicht genügend Einfluss nehmen können. Nun aber bekamen sie mächtig Rückenwind durch die gesteigerte Aufmerksamkeit von Öffentlichkeit und Administration.

Die Kultusbehörden reagierten sehr unterschiedlich auf die Computer im Mathematikunterricht, die Palette reichte von pflichtmäßigem Einsatz von Computer-Taschenrechnern (Sachsen) über Ermunterung und Duldung bis zum Verbot (Bayern). Niedersachsen brach durch eine Pflichtfortbildung der Mathematikkollegien der Gymnasien die Mauer der Ignoranz auf und unterstützte dadurch die fortschrittlichen Kräfte.

 

Was sind denn Computerwerkzeuge im Mathematikunterricht?

Man unterscheidet verschiedene Typen:

ü      GTR, Graphikfähige Taschenrechner. Sie können über die üblichen TR hinaus noch alle schulischen Funktionen und Funktionenscharen zeichnen. Die entsprechenden Graphen können die Lernenden interaktiv erkunden und für alle schulisch üblichen Fragen (Maximum, Nullstelle, Integral u.s.w.) numerische Antworten erhalten. Spiralen, dreidimensionale Flächen, Folgen, Reihen und statistische Daten lassen sich untersuchen, Gleichungen und Gleichungssysteme lösen und vieles mehr. In Niedersachen sind GTR ab Klasse 7 Pflicht (seit 2002).

ü      TK, Tabellenkalkulationssoftware, z.B. Excel, ist ein numerisch arbeitendes umfassendes Werkzeug, das viel Eigentätigkeit der Lernenden ermöglicht. Besonders augenfällig wird hier der Zusammenhang von Formel, Wertetabelle und graphischer Darstellung. Nicht zu unterschätzen ist auch der Vorteil, dass Excel (oder ähnliche TK) für die Lernenden zuhause und in der Berufswelt -und das sogar weltweit- verfügbar ist. (Kürzlich hat jemand in China die Excel-Schieberegler aus meinen Internetseiten eingesetzt und sich mit einem Foto seiner chinesischen Studierenden bedankt.) TK-Unterrichtseinheiten sind Pflicht in Niedersachsen (Sek I Gy)

ü      DGS, Dynamische-Geometrie-Systeme. Sie haben die Lehrerschaft sofort überzeugt, da ganz offensichtlich damit ein beweglicher Geometrieunterricht möglich wird. Man kann mit Kreisen, Senkrechten, Parallelen u.s.w. konstruieren, z.B. den Inkreis eines Dreiecks. Wenn man dann aber an einer Ecke des Dreiecks zieht, verändert sich dessen Form, aber der Inkreis bleibt stets Inkreis. Sie haben eine Renaissance der Schulgeometrie eingeleitet, worüber ich 2004 an unserer Universität eine Sonntagsvorlesung gehalten habe. Auch DGS-Unterrichtseinheiten sind Pflicht in Niedersachsen (Sek I Gy).

ü      CAS, Computer-Algebra-Systeme. Sie sind die umfassendsten und mächtigsten Werkzeuge und lassen sich aus der Mathematik und allen Mathematik verwendenden Wissenschaften nicht mehr wegdenken. Über alle numerischen Antworten wie sie GTR und TK geben hinaus können sie auch symbolisch auf jedem Niveau mit Mathematik umgehen, vorausgesetzt der Nutzer weiß, was er machen könnte und was dann die Antwort bedeutet. Ohne dass er seine Frage mathematisch formulieren kann, erhält er vom CAS keine Antwort.
Die gängigen CAS sind heute Derive, MuPad, Maple und Mathematica. Mit Derive, das es seit 1989 gibt, kennt man sich im Schulbereich am besten aus, es gibt auch schon reichlich didaktische Forschung, besonders aus Österreich, und schulisch brauchbares Material.

ü      CAS-Handheld, Taschenrechner mit CAS, TK und DGS,
(TI voyage, Casio Classpad).
Diese mächtigen Taschencomputer sind kaum größer als gewöhnliche Taschenrechner und wurden (seit 1995) für den schulischen Alltag entwickelt. Die fachdidaktische Forschung hat nachgewiesen, dass die Kompetenzsteigerung eines entsprechenden Unterrichts bei ständiger Verfügbarkeit solcher Werkzeuge am größten ist. Da auch CAS-Unterrichtseinheiten Pflicht in Niedersachsen (Sek I Gy) sind, sind etliche Gymnasien, z.B. das Johanneum in Lüneburg, zur Einführung eines CAS-Handheld übergegangen und erfüllen damit alle Anforderungen.

ü      DMS Dynamische-Mathematik-Software, ein Name der noch nicht etabliert ist, der aber beschreibt, dass es in allen genannten Computerwerkzeugen in zunehmendem Maße die Möglichkeit gibt, Graphiken beweglich zu gestalten.
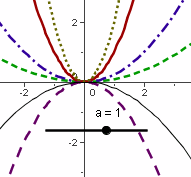
Hervorstechendes Merkmal sind die Schieberegler, bei denen man mit der Computermaus einen Paramterwert variiert und so eine davon abhängige Form kontinuierlichverändern kann. (Schülerin: Ich lasse meine Parabel erstmal Gymnastik machen.) Auch weiter entwickelte DGS, die Analysis, Algebra und Geometrie verbinden (GeoGebra, www.geogebra.at), gehören in diese Kategorie. Sie lassen Lernenden und Lehrenden besonders viel Freiheit in den Realisierungsmöglichkeiten und man kann schier alles bewegen, eben: Mathematik in Bewegung

 

Was sind nun Merkmale eines gewandelten Mathematikunterrichts?

Natürlich gab es auch schon vor der Computerzeit hervorragenden Unterricht, der nach besten Kräften die unten dargestellen Ziele verfolgte. Es überwog aber oft die nicht ganz unberechtigte Befürchtung, dasszuviele Freiheiten für die Lernenden zu langen und unüberschaubaren Rechnungen führen könnten. Den renommierten Didaktiker Hans Schupp habe ich aber 1996 sagen hören: Diese Werkzeuge zwingen uns dazu, den Unterricht zu machen, den wir längst hätten machen sollen.

Es geht also um entdeckendes Lernen, um eigenständige Erkundung und Prüfung seitens der Lernenden, um Visualisierungen, die Verstehen ermöglichen.

 

 

Beispiel: Unterstützung grundlegender Einsichten

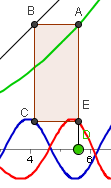Die Verkettung von Funktionen lässt sich für jede Stelle x mit einem Fähnchen visualisieren. In Abbildung 1 ist das für f(x)=g(h(x))=sin(x²) dargestellt.

Stets geht man von der Stelle x zur inneren Funktion, hier A. Den so erhaltenen Wert muss man ja nun in die äußere Funktion einsetzen. Das macht man graphisch: man geht zur Winkelhalbierenden, hier zu B, zur äußeren Funktion, hier zu C. Diesen Endwert überträgt man zu E und endet über oder unter der Startstelle. Dieses Vorgehen erzeugt auch an der Schultafel schon Einsichten, es wird aber deutlich eindrucksvoller, wenn die Lernenden den Punkt D selbst verschieben können.

Man lässt dabei zuerst E seine die Ortskurve zeichnen. Wird danach der Graph von f direkt durch Termeingabe erzeugt, so zeigt sich die Richtigkeit des Konzeptes. Dessen Kraft entfaltet sich nun dadurch, dass durch Betrachtung von Nullstellen, Wert-1-Stellen u.s.w der gesamte Verlauf der verketteten Funktion begriffen und begründetwerden kann. Dadurch wird die Überlegenheit mathematischen Argumentierens über die oft unzureichende Darstellung im Graphenzeichner augenfällig. Doch damit nicht genug: im Werkzeug GeoGebra (www.geogebra.at) lassen sich Funktionsgraphen, z.B. die Parabel durch A, mit der Maus anfassen und frei verschieben. Der Graph der Verkettung wandelt prompt seine Form und gibt zu vielerlei Beobachtungen Anlass. Last but not least kann jede Funktion in jede andere umdefiniert werden, so dass die Generalisierung in eigentätigem Erkunden erfolgen kann.

Dieses Beispiel kann auf meiner Site www.mathematik-verstehen.de im Bereich Didaktik, Funktionen und Graphen interaktiv erfahren werden.

 

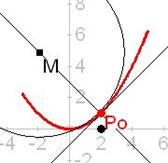Beispiel: Dynamische Bildung des Begriffs Krümmung

Nachdem in einer unterrichtlichen Situation geklärt wurde, dass man sinnvollerweise von Krümmung in einem Punkt P sprechen muss, dass ein Kreis gesucht ist, der die Tangente in P berührt, kann man die in Abbildung 2 dargestellte Situation in einem DMS erzeugen oder vorbereitet einsetzen. Durch Ziehen an M vor aller Augen wird die Frage aufgeworfen:

Welcher der kleineren und größeren Kreise soll denn nun mit Recht der Krümmungskreis heißen?. Einhellig wird der Kreis als bester akzeptiert, der die Kurve in P durchsetzt. Da auch die Taylorpolynome 2. Grades i.a. die Kurvengraphen im Entwicklungspunkt durchsetzen, kommt man auf die Idee, die Übereinstimmung der 2. Ableitung von Krümmungskreis und f in P zu fordern. Zusammen mit den oben schon genannten Bedingungen folgt die bekannte Krümmungsformel. Dabei geht noch ein, dass Kreise konstante Krümmung haben müssen und dass diese dann der Kehrwert von r sein muss.

 

These: Bewegung beflügelt Verstehen

Die Krümmungsformel kann man unverstanden lernen. Die Dynamik aber kann man sehen, einsehen und behalten. Erst durch die Bewegung entsteht das Objekt, der Krümmungskreis bzw. die verkettete Funktion. Übertragungen auf andere Funktionen sind sehr leicht möglich und die Begriffsbildungen werden so gefestigt. Die Lernenden können durch die kontinuierliche Veränderung einen Überblick über ganze Funktionenklassen gewinnen. Ein bisher übliches Ergebnis wie: Die Wendestelle ist bei 4,711 wird unwesentlich gegenüber einer von den Lernenden gewonnenen Erkenntnis wie: Alle Polynome 3. Grades sind symmetrisch zu ihrem Wendepunkt. Entscheidend ist, dass da kein Unterrichtsfilm abläuft, sondern dass die Werkzeuge offen sind, die Erkundung (weitgehend) eigenständig geplant wird und die Variation selbst in die Hand genommen wird.

 

Weitere Aspekte eines Mathematikunterrichts mit Computerwerkzeugen.

ü      Genderaspekte: Vor allem den Mädchen kommt das Erarbeiten von Überblicken sehr entgegen und es baut auch ihre Angst vor Überraschungen ab. Eine anderer Lerntyp, oft sind es Jungen, ist mit der Erzeugung irgendwelcher Zahlen schnell zufrieden. Auch hier tut es gut, durch Generalisierung und Klassifizierungen den Einzelfall zu relativieren.

ü      Modellierungs- und Problemlöse-Aspekte: Durch die Werkzeuge kann ein Modellierungskreislauf leicht mehrfach und auch variantenreich durchlaufen werden. Lösungen sind dennoch in überschaubarer Unterrichtszeit möglich. Es wird der Mut gestärkt, Probleme auch dann anzugehen, wenn noch keine Lösung gelernt wurde.

ü      Methodische Aspekte: Auf Arbeit in Gruppen, an Stationen, mit Lerntagebüchern u.s.w. kann hier nicht eingegangen werden. Es ist aber klar, dass viele kreative Ansätze ihr lohnendes und reichhaltiges Feld finden können. Auch inhaltlich kann auf diesen wenigen Seiten nicht dargestellt werden, wie ein solches Konzept der Visualisierung und Variation wirklich alle Themen durchziehen kann.

ü      Lernpsychlogische Aspekte: In konstruktivistischem Sinn muss Unterricht den Lernenden helfen, die Begriffe richtig zu bilden und kompetent zu nutzen. Da die Beurteilung von richtig und falsch nicht mehr fast ausschließlich durch die Lehrenden erfolgt, können sich die Lernenden als eigenständig Handelnde erfahren. Die Lehrenden werden stärker zu Helfern bei Problemen. Sie verlieren auch ihren Allwissenheitsnimbus, denn leicht können die Lernenden Wege gehen, die nicht geplant waren.

ü      Mathematische Aspekte: Die enorme Reichhaltigheit der Mathematik kann entschieden deutlicher werden. Mathematik lebt vom kreativen Handeln, vom Durchdringen der Strukturen, vom Problemfinden und Problemlösen. Unverstandene Mathematik ist zu gar nichts nütze.

ü      Gesellschaftliche Aspekte: Schließlich hat der herkömmliche Mathematikunterricht die Brille hergestellt, durch die die Gesellschaft heute die Mathematik in wenig rosigem Licht sieht. Ein Umdenken kann nur duch bessere Erfahrungen eingeleitet werden. In der komplexer und anspruchsvoller werdenden Welt können wir nicht bestehen, wenn die Zahl der Mathematikflüchtlinge weiter wächst. Noch nicht einmal in der Welt der Ingenieure und Ökonomen reicht heute und in Zukunft das Ausrechnen-Können. Das machen nämlich die Computer. Gefragt sind Beurteilung und Ergebniskritik, Antizipation, was die Computer zeigen müssten, und vernünftiges Handeln, wenn sie es nicht tun.

 

Was folgt daraus für die universitäre Lehrerausbildung in Mathematik?

In der Mathematik tritt der Wissenserwerb weit hinter die Entwicklung einer Denk- und Handlungskompetenz zurück. Dies zeigen auch Untersuchungen zu den Arbeitsfeldern von Diplommathematikern. Für das Lehrerstudium muss das aber in besonderem Maße gelten, denn wenn in der Schule Lehrende ihr Wissen nicht durchdrungen haben sondern es nur vortragen, ist Lernen fast unmöglich.

Die Hochschullehre in der Mathematik stellt sich diesem Anspruch und kann es in Lüneburg in besonderem Maße mit Blick auf Schule tun, da nicht gleichzeitig Diplommathematiker ausgebildet werden müssen. Die Veranstaltungen, die gemeinhin Vorlesungen genannt werden, beziehen Computerwerkzeuge ganz selbstverständlich ein, bieten Visualisierungen auf jedem mathematischen Niveau und geben den Studierenden vor allem Gelegenheit, sich einem Zusammenhang oder einem Begriff erst anzunähern und ihn zu begreifen, bevor er bewiesen und in seiner mathematischen Relevanz eingeordnet wird. Die Eigentätigkeit der Studierenden wird weiter angeregt durch die Arbeit mit Computern im oben beschriebenen Sinne, unterstützt durch das Internet, wo Anregenungen und Lösungen auf unseren Seiten www.mathematik-verstehen.de verfügbar und reichhaltige einschlägige Seiten zu finden sind.

Eine Intensivierung dieser Unterstützung scheitert an unserer notorischen Personalknappheit. Allerdings haben wir etliche TI-voyage (CAS-Handhels, s.o.) zum Ausleihen, so dass jeder Studierende entprechende Kompetenz erwerben muss. In allen Klausuren inclusive dem Staatsexamen sind die mächtigen Geräte erlaubt. Damit gehen wir den Weg konsequent, den Niedersachsen u.a. Länder in ihrem Zentralabitur ermöglichen.

Auch die Veranstaltungen zur Fachdidaktik bieten hier Begleitung und Fundierung und bringen eine geänderte Unterrichts- und Aufgabenkultur auf den Weg.

 

Fazit

Mathematikunterricht ist wie ein Tanker, der nur gaaaanz langsam seine Richtung ändert. sagte W. Löding aus Hamburg vor einigen Jahren. Gerade weil ich zu den Motoren gehöre, die vor mehr als 15 Jahren diese Bewegung eingeleitet haben, werde ich sie jetzt in der Lehrerausbildung nach Kräften unterstützen. Nach einem Vierteljahrhundert Erfahrung in Schule, Lehrerfortbildung, Lehrer- und Ingenieurausbildung weiß ich auch, welches Potenzial hier steckt. Unsere Absolventen setzen diese durch den Werkzeuggebrauch veränderte Únterrichtskultur in Praktika, im Studienseminar und in ihrer Schule mutig in die Tat um. So sind in den vergangenen zehn Jahren von der Universität Lüneburg Impulse in die Schulen getragen worden, die den Mathematikunterricht bewegen.