Mathematik Verstehen Dörte Haftendorn: Fraktale Geometrie, Wegfraktale rekursiv

Prof. Dr. Dörte Haftendorn

[LBS-Mathe] [Fraktale Geometrie]

Download des MuPAD-Notebooks Save Link Taget As..., Verküpfung speichern unter...

Fraktale mit MuPAD, Eigene Lindenmayersysteme
Prof. Dr.Dörte Haftendorn, April 03,
________________________________________________________________________________

Inhalt....: Erzeugung von Fraktalen mit Lindenmayersystemen eigne Version
Kategorie.: Arbeitsblatt
Mathematik: Fraktale Geometrie
MuPAD.....: 2.5.0

Wegfraktale mit Turtlegrafik

im Vergleich mit Version 2.5
Datum.....: 2003-04-24
Autoren...: Dörte Haftendorn <Haftendorn@uni.leuphana.de>
Funktionen: plot, plot::Lsys, plot::Turtle
________________________________________________________________________________
LEVEL 1
Die Grundidee der Lindenmayersysteme ist folgende:
1. Es gibt gerade Striche, symolisiert durch F, "die Turle läuft Forward".
2. Es gibt gerade Vorwärtssprünge, symolisiert durch f, "die Turle springt forward".
3. Es gibt einen Winkel w, um den die Turtle ihre Richtung ändern kann,
+ dreht w Grad nach links, - dreht w Grad nach rechts.
4. Mit [ merkt sich die Turtle ihre momentane Position. Bei ] kehrt sie dahin zurück.
5. Es gibt ein Startelement, ein "Axiom", einen Initiator, zum Beispiel einen geraden Strich F.
6. Es gibt eine Liste von "Regeln", nach denen die vorkommenden Zeichen erstetzt weden.
7. In einer "Generation"= Iterations-Stufe = Iterations-Schritt werden alle Regeln "auf einen Schlag" angewandt.
8. Das so entstehende "Lindenmayer-Wort" wird dann von der Turtle als Laufanweisung "abgearbeitet".

F:=proc() begin T::line(x)end_proc:
f:=proc() begin T::move(x)end_proc:
R:=proc() begin T::right(w)end_proc:
L:=proc() begin T::left(w)end_proc:
K:=proc() begin T::push()end_proc:
Z:=proc() begin T::pop()end_proc:
Gr:=proc()begin T::color(RGB::Green)end_proc:
Bk:=proc()begin T::color(RGB::Black)end_proc:
Rd:=proc()begin T::color(RGB::Red)end_proc:
Ma:=proc()begin T::color(RGB::Magenta)end_proc:

Kochkurve
F( ) ist der Initiator.
Für die jeweils nächste Stufe wird jedes F( ) durch den Generator F( ):L( ):F( ):R( ):R( ):F( ):L( ):F( ):
ersetzt. Erzeugung "von Hand":

x:=1:w:=60:T := plot::Turtle(): T::right(90):
F():L():F():R():R():F():L():F():
plot(T, Axes = None,Scaling=Constrained):

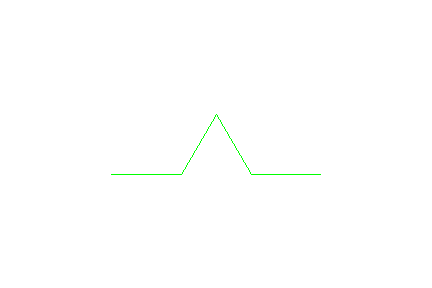
x:=1:w:=60:T := plot::Turtle(): T::right(90):
F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():
plot(T, Axes = None,Scaling=Constrained):

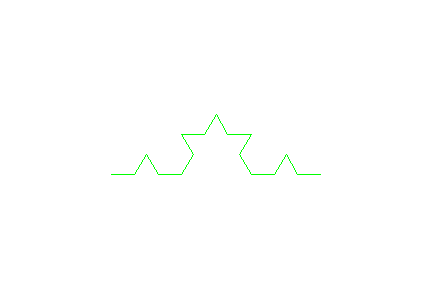
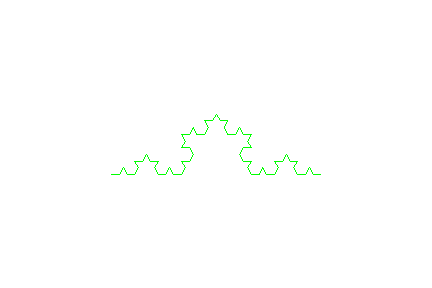
x:=1:w:=60:T := plot::Turtle(): T::right(90):
F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():
L():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():
R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():
L():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():R():R():F():L():F():R():R():F():L():F():L():F():L():F():R():R():F():L():F():
plot(T, Axes = None,Scaling=Constrained):

F wird F-F++F-F , das wird dann zu F-F++F-F - F-F++F-F ++ F-F++F-F - F-F++F-F
da wird dann wieder jedes F durch die Regel erstetzt.
----------------------------------------------------------------------------------------
Da die Lindenmayerworte so schnell wachsen, ist hier noch etwas Programmierarbeit angesagt.

"Quadro-Kochkurve"
Stufe 2 zeigt immer den "Generator", die Figur die den Initiator ersetzt.

L := plot::Lsys(90, "+F", "F"="F-F+F+F-F"):
L::generations := 2:
plot(L, Axes = None,Scaling=Constrained)

Gemeinsame Erzeugung mehrerer Generationen (Stufen)

for g from 2 to 5 do
L::generations := g:
plot(L, Axes = None,Scaling=Constrained)
end_for:

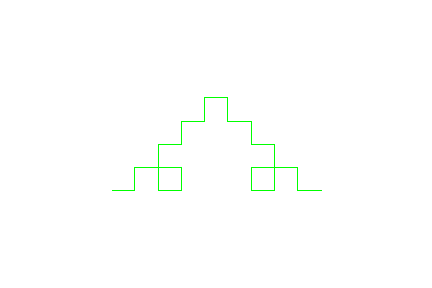
Zweig

delete(L):
L := plot::Lsys(33,"F","F"="F[-F]F[+F]F"):
L::generations := 2:
plot(L, Axes = None,Scaling=Constrained)

delete(L):
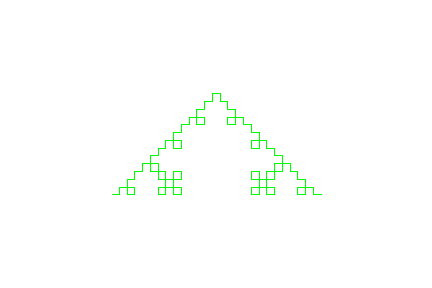
L := plot::Lsys(20,"F","S"="FF","F"="F[-F]F[+F]F"):
L::generations := 4:
plot(L, Axes = None)

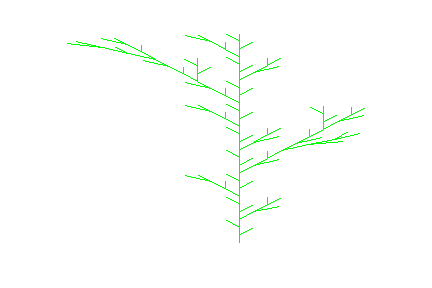
L := plot::Lsys(90, "F-F-F-F",
"F"="F-F+F+FF-F-F+F"):
L::generations := 2:
plot(L, Axes = None)

Lindenmayersysteme aus der MuPAD-Hilfe

L := plot::Lsys(90, "F", "F"="FF-F--F-F"):
L::generations := 5:
plot(L, Axes = None)

L := plot::Lsys(90, "F-F-F-F", "F"="FF-F--F-F"):
L::generations := 4:
plot(L, Axes = None)

L := plot::Lsys(90, "F-F-F-F", "F"="FF-F+F-F-FF"):
L::generations := 4:
plot(L, Axes = None)

L := plot::Lsys(90, "L", "L"="L+R+",
"R"="-L-R", "L"=Line, "R"=Line):
L::generations := 10:
plot(L, Axes = None)

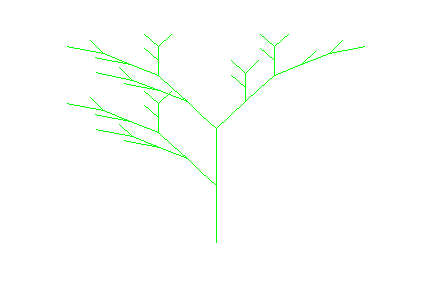
L := plot::Lsys(20, "L", "L"="R[+L]R[-L]+L",
"R"="RR", "L"=Line, "R"=Line):
L::generations := 4:
plot(L, Axes = None)

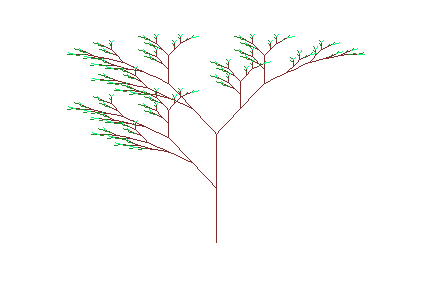
L := plot::Lsys(20, "L", "L"="BR[+HL]BR[-GL]+HL", "R"="RR",
                "L"=Line, "R"=Line,
                "B"=RGB::Brown, "H"=RGB::ForestGreen,
                "G"=RGB::SpringGreen):
L::generations := 6:
plot(L, Axes = None)

L := plot::Lsys(60, "F++F++F", "F"="F-F++F-F"):
L::generations := 5:
plot(L, Axes = None)

Internetadressen dieses Web-Verbundes [www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math]
[LBS-Mathe] [Fraktale]
Inhalt und Webbetreuung Prof. Dr. Dörte Haftendorn Apr. 2003, update 16. August 2011

Lindenmayersysteme aus der MuPAD-Hilfe