Teufelstreppe

Teufelstreppe stufenweise		Dimension	LOGO	Galerie der Wegfraktale
Rechnungen	Fazit	Didaktik	L-System	Leitseite der Wegfraktale

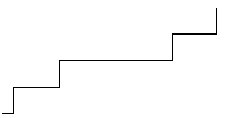
1. und 2.,
3. und 4.
und 5. Stufe

Hier stellt man sich die Stufe 1 als Inititator (Startfigur) vor.
Dabei ist die große waagerechte Stufe dreimal so lang wie einleitende Stufe, dieses kurze Element sei b.
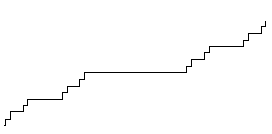
Die einleitende Stufe wird bei jedem Schritt auf 1/3 ihrer Länge gekürzt. Die anderen waagerechten Elemente werden beibehalten. Bei jedem Schritt in jede Senkrechte in der Mitte die einleitende Stufe waagerecht eingefügt.
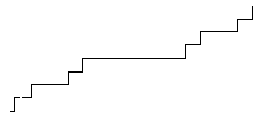
Daher wird die Teufelstreppe bei jedem Schritt breiter, aber nicht höher.
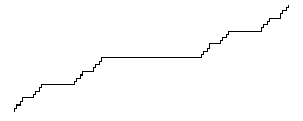
Die Breite wird durch folgende geometrische Summe beschrieben:
Breite = b ( 3 + 1 +2/3 + 4/9 + 8/16 + ....) = b ( 3 +1/(1-2/3)) = 6 b
Trotz dieser endlichen Breite, die nur das Doppelte der großen Anfangsstufe ist, wächst die Stufenzahl der Teufelstreppe ins Unendliche. (Achtung, es gibt auch leicht abweichende Definitionen der Teufelstreppe)

Daher ist die Teufelstreppe ein Fraktal.

Dimension
Die Teufelstreppe ist nicht streng selbstähnlich. Versucht man, verkleinerte Kopien ihrer selbst zu finden, so stören die gleichlang bleibenden Stücke und die Verschiedenheit der Stauchfaktoren für senkrechte und waagerechte Längen.
Mit der Selbstähnlichkeits-Dimension kommt man also nicht zurecht.

Bei einer Messung der Boxdimension wird vermutlich etwa d=1 herauskommen.
Didaktik

Die Teufelstreppe läßt sich recht leicht auf Karopapier zeichnen. Die Überlegung zur Breite ist im Thema geometrische Reihen sinnvoll. Sie ist ein schönes Beispiel dafür, dass Fraktale zwar ihren Namen von der möglicherweise nichtganzen (gebrochenen) Dimension haben, dass es aber auch Fraktale mit Dimension 1 gibt.

Lindenmayer-System

Axiom A

Regeln A geht auf ABA

Der Baustein B tritt als eigene Prozedur auf.

B geht auf BBB

Deutung A=F+V-

B=FFF

+=90° links -= 90° rechts

F und V erscheinen als vorwärts-Befehle mit Schrittweiten a bzw. h
a wird bei jedem Schritt gedrittelt, h wird halbiert.

Berücksichtigt man die Deutung, so kann man das Axiom in der Abbruchbedingung der Rekursion wiedererkennen.

Weg-Prozeduren mit Igelgraphik Hier gezeigt in LOGO, ebenso geht es mit Turtlegraphik in Pascal.

PR teufel :n :b :a
wenn :n = 0 dann vw :b li 90 vw :a re 90 rk
teufel (:n-1) (:b/3) (:a/2)
teufelmitte (:n-1) (:x/3)
teufel (:n-1) (:b/3) (:a/2)
ENDE

PR teufelmitte :n :b
wenn :n=0 dann vw 3*:b rk
teufelmitte (:n-1) (:b/3)
teufelmitte (:n-1) (:b/3)
teufelmitte (:n-1) (:b/3)
ENDE

Fazit: L-Systeme lassen sich in rekursive Weg-Prozeduren übersetzen. Hier ist dies für ein Beispiel ohne Knoten gezeigt. In Pascal lassen sich auch die Knoten einfach rekursiv verwalten. In LOGO ist es vernünftig, eine dynamische Liste für die Knotenkoordinaten zu eröffnen.
Die naheliegende Versuch, das Lindenmayerwort wirklich zu bilden, stößt leider sehr schnell an die Grenzen der Speichermöglichkeiten. Man muß es während seiner Bildung sofort "abarbeiten".-

Selbstähnlichkeitsdimension

Galerie der Wegfraktale

Leitseite Wegfraktale

[Fraktale (Leitseite)] [Wegfraktale] [Galerie] [Programme]

(1996)(2002) Apr. 2005, update 16. August 2011

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]