[www.mathematik-verstehen.de] Analysis Leitseite URL haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/analysis.htm

[Didaktik] [Computer] [Funktionen und Graphen]   [Geometrie] [Kreissätze] [MuPAD]   © Prof. Dr. Dörte Haftendorn

download Ziel speichern unter....

Sehnensatz algebraisch bewiesen
Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Nov. 05 Update 23.11.05
Web: www.mathematik-verstehen.de haftendorn.uni-lueneburg.de/ing-math
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben
Es geht um den Sehnensatz
Für einen algebraischen Beweis kann man o.B.d.A. den Kreis in den
Mittelpunkt und den Schnittpunkt p der Sehnen aus die pos. y-Achse legen.
Grundlegend: Behauptet wird, dass das Produkt der Sehnenabschnitte beliebiger
Sehnen gleich ist. Das heißt, dass es konstant ist, wenn P festliegt. Diese Konstante muss
nun i*j sein, denn JK ist auch eine mögliche Sehne.
Es gilt:

• j:=sqrt(r^2-p^2); i:=j; i*j;

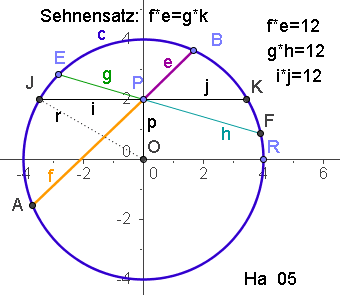
Zu zeigen bleibt also: f*e=j^2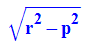

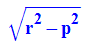
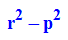
• sek:=x->m*x+p

• kreis:=(x^2+y^2=r^2)

• sekInKreis:=subs(kreis, y = sek(x));

• assume(m,Type::Real)

• ab:=solve(sekInKreis,x);

Die Behauptung wird in quadrierter Form bewisen: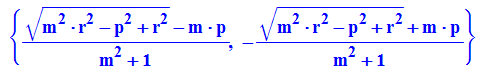

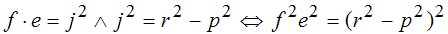
• ab[1] //links Schnittstelle

Da m die Steigung ist, gilt für ein Steigungsdreick, dass x1 breit ist,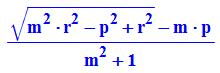
dass es m*x1 hoch ist. In einem solchen Steigungsdreieck ist f die
Hypothenuse und Pythagoras sagt das Folgende:

• fq:=(1+m^2)*ab[1]^2;eq:=(1+m^2)*ab[2]^2; Jetzt 3. Binomische Formel anwenden, nicht 1 und 2.!!!!!!!

• fq*eq

• simplify(%)

Damit ist der Sehnensatz algebraisch-analytisch bewiesen.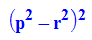
Zu Bedenken bleibt, dass der geometrische Beweis mit dem Umfangswinkelsatz
erheblich griffiger ist.
Warum zum Teufel glaubt man, Term-Turnen sei besser als Geometrie-Treiben?.

[Kreissätze] [Analysis] [Geometrie] [Computer] [MuPAD] [ing-math]

Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Nov. 2005, update 23. November 2005

Direkte Internetadressen [www.doerte-haftendorn.de]    [www.mathematik-verstehen.de]