
Setze den Punkt Q zugfest auf g
und hebe das Dreieck ABQ durch fette Linien hervor.
Speichere dieses Dreieck, denn es ist die Grundlage einer ganzen Aufgabenfamilie.
Probe: Wenn man an Q zieht wird das Dreieck nur geschert, g muss fest bleiben. Wenn man V bewegt, darf g nur parallel verschoben werden, hier also nur auf und ab parallel zu AB bewegt werden.

2) Konstruiere den Höhenschnittpunkt.
Prüfe, ob der Höhenschnittpunkt zugfest ist.
Wähle einen neuen Namen für diese Zeichnung und speichere sie.
Lasse Q auf der Straße g wandern und erzeuge die Ortslinie von P
Handwerk:
Setze Spur für P bei F7 (Trace), F1 oder ESC, dann zu Q laufen (This Point) Hand drücken, gedrückt halten und Q mit den Cursortasten ziehen. Besonders für die neueren TI ist das die beste Art.Alternativ: Setze Spur für P bei F7 (Trace), dann F7 Animation, Q anklicken, Hand drücken, gedrückt halten und Q mit den Cursortasten ziehen. Dabei bewegt sich Q nicht. Man kann sich vorstellen, dass man wie bei einer Zwille Energie in Q pumpt, lässt man nun los, wandert Q auf seiner Straße und P malt seine Kurve. Das geht solange, bis man enter drückt.
Alternativ: Ortskurve vom TI rechnen lassen. F4 Locus, P anklicken, Q anklicken, Abwarten, bis in der Statuszeile BUSY verschwindet. Die Ortskurve erscheint als Objekt. Wenn sie zu sehr wie ein Streckenzug aussieht, muss man bei F8 Format, # of Locus Points, eine höhere Zahl wählen.
Bemerkung: Im Gegensatz zu anderen DGS kann man bei Cabri auf die Ortslinie sogar zugfest Punkte setzen.
|
Experimentieren, Beobachten und Nachdenken soll die Fragen klären helfen. |
|
|
Lösungen |
Halt, nicht vor dem Ausprobieren ansehen!!!!!!!!!!!!!!!!!!!!!!!!!!! |
A)


B)
A und B müssen auf der Ortslinie liegen, denn wenn das Dreieck bei A bzw. B rechtwinklig ist, ist A bzw. B selbst der Höhenschnittpunkt P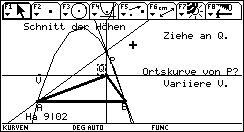
Varianten: Statt zweier Höhen kann man beliebige Kombinationen aus Dreiecksgeraden probieren,
z.B. wh mit sh... (siehe Weth)
Datei parall3eckhoehoevoy.doc[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt] |