Zu Arbeitsblatt Klasse 8, Konstruktion 4, Kissoide

Download als pdf- Arbeitsblatt (Ab Klasse 8)
Zum Kurven-Arbeitsblatt

Konstruktion 4

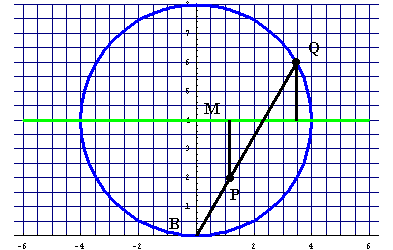
P liegt auf der Geraden BQ und hat von der waagerechten Geraden denselben Abstand wie Q. Das kann man durch Abzählen von Karos feststellen.

Wenn Q auf dem Kreis wandert, bewegt sich P auf einer "Kissoide", einer "Efeu-Kurve".

Erzeuge weitere Orte für Punkt P.

Realisierung in Schritten im DGS Dynageo-Euklid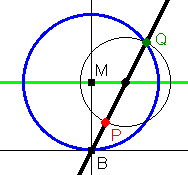

Erzeuge zuerst das rechtwinklige Kreuz bei B.
Du kannst das Koordinatenkreuz nehmen.
Setze M zugfest auf die Senkrechte, der blaue Kreis muss durch B verlaufen.
Setze Q zugfest auf den Kreis, <
verbinde BQ mit einer Geraden, probiere ob alles zugfest ist.
Wähle mit dem Schnittpunkt-Werkzeug den Mittelpunkt des kleinen Kreises und konstruiere so P.

Überlege, warum damit die oben geforderten Strecken gleich lang sind.

Ziehe an Q und beobachte P, vergleiche mit deiner Von-Hand-Konstruktion oben.

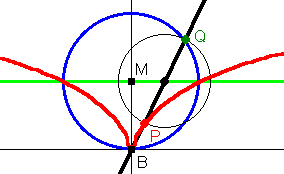Erzeuge die Ortskurve von P.

Handwerk: Icon "Ortslinie aufzeichnen", P klicken, Q ziehen.

Diese Kurve heißt "Kissoide" oder "Cissoide".

Die Griechen nannten sie so nach der Spitze, die ein Efeublatt hat (cissos=Efeu).
Welche besonderen Eigenschaften der Ortskurve kannst du erkennen.
Prüfe durch Ziehen an M, ob die von dir gefundenen Eigenschaften zugfest sind.

Lösung: Die Kissoide kann nicht höher steigen als bis zur waagerechten Geraden durch den höchsten Punkt des Grundkreises. Man sagt, sie hat eine Asymptote. Weiteres s.u.

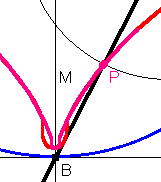
Die tropfenförmige (rote) Spitze fand Mathix, als er das obere Bild vergrößerte. Mathilde hat in der vergrößerten Version die Ortskurve nochmals gezeichnet. Sie wurde spitzer.

Wie ist es denn nun? Reicht sie genau bis B? Ist sie spitz?

Lösung: Die Kissoide erreicht B, denn wenn Q ganz oben auf dem Kreis ist, muss P ganz unten, nämlich in B, sein. Computer zeigen nicht immer alles!!!!

Wenn Q im Uhrzeigersinn auf dem Kreis wandert, läuft P in einer Linkskurve auf B zu. Der Kreis ist ganz gleichmäßig, es ist kein Grund zu sehen, warum bei B eine kleine Rechtskurve sein sollte. Nach B ist es auch eine Linkskurve.

Kl8konstr4Kissiode.doc

Konstuktion 4
Kissoide