Algebraische Kurven URL haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/kurven.htm
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]    © Prof. Dr. Dörte Haftendorn

Konzipiert nach dem Arbeitsblatt zu Algebraischen Kurven. Das zuvor eingesetzte Arbeitsblatt enthielt die Konstruktion 5 nicht, denn die sollte hier in der Klassenarbeit erst folgen.
Die ersten beiden Aufgaben waren zu üblichem Klammer-Thema gestellt.

Mathematik Klassenarbeit Nr.2 Kl 8 FL Ha Name:

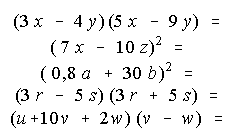
Aufgabe 1) Löse die Klammern auf und fasse zusammen:



Aufgabe 2) Faktorisiere, wenn es mit binomischen Formeln geht. Klammere vorher aus, falls es nötig ist. Prüfe schriftlich den Mittelterm.

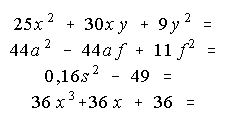
Aufgabe 3)

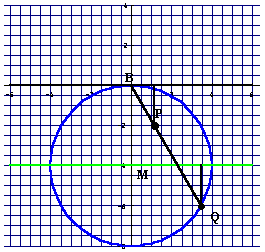Konstruktion:

P liegt auf der Geraden BQ und hat von der waagerechten Geraden durch B denselben Abstand, den Q von der waagerechten Geraden durch M hat. Das kann man durch Abzählen von Karos feststellen.

Wenn Q auf dem Kreis wandert, bewegt sich P auf einer Strophoide, d.h. "Seil-Kurve".

a)

Erzeuge weitere Punkte, mindestens 10, darunter einige in dem Bereich über B. Verbinde die Punkte.

Hat die Kurve eine Symmetrieachse?

b) Dieses Blatt ist rechts und links sicher zu klein. Ist es oben auch zu klein? M.a.W.: wächst die Strophoide über Höhe 4 hinaus?

c)

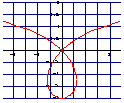
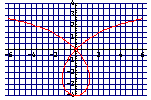
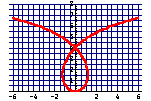
Welche dieser Strophoiden ist die, die du oben konstruieren solltest? Woran erkennst du das?



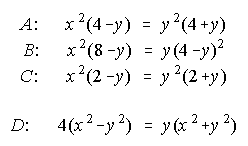
d) Die Gleichungen A, B und C gehören zu den drei Strophoiden.

Ordne begründet richtig zu.

e) Gleichung D ist eine Umformung von einer der Gleichungen A, B oder C. Entscheide von welcher Gleichungen D stammt und führe die Umformung schrittweise durch.
[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  (1998), Apr. 2002, update 16. August 2011
Direkte Internetadressen
[www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]