www.mathematik-verstehen.de
© Prof. Dr. Dörte Haftendorn

Link zum Buch
Site-Info
URL  http://haftendorn.uni-lueneburg.de/mathe-lehramt/kurven/tranzendente/traktrix/traktrix.htm
[Kurven]  [Tranzendente Kurven]  [Computer]

Traktrix

Im Kurvenprojekt Kl. 8 Erklärung von Leibnitz und weitere Informationen zur Traktrix
[Graphics:traktrix-b/traktrix_1.gif] Integrationen und Zeichnungen mit Mathematica

Richtungsfeld und numerische Lösung,
Mathematica, Web
Download Mathematica-Notebook Traktrix mit Richtundsfeld
DownloadTraktrix als DGL Mathematica-Notebook

Und nun seit Sept 05 besonders einfach mit MuPAD 3.11
Traktrix als Sonderfall der Fahrradkurven, dort ausführliche Numerische Lösung mit Richtungsfeld 		Herleitung der DGL

Handschrift-Seite
Herleitung der DGL
in Parameter-Darstellung

Handschrift-Seite
Variante der Fragestellung Normale statt Tangente Download Mathematica-Notebook

Traktix mit Differentialgleichungen

Prof. Dr. Dörte Haftendorn, Universität Lüneburg, Mai 2004

[Graphics:traktrix-b/traktrix_1.gif]

•Linienerzeugung in der Datei trakrix.nb

•DGL

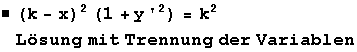
•(k - x)^2 (1 + y '^2) = k^2       Lösung mit Trennung der Variablen

yyy = -∫ (1/z) (k^2 - (z)^2)^(1/2) d z

k log((2 (k^2 - z^2)^(1/2))/(k^2 z) + 2/(k z)) - (k^2 - z^2)^(1/2)

yyy // Simplify

k log((2 (k + (k^2 - z^2)^(1/2)))/(k^2 z)) - (k^2 - z^2)^(1/2)

c = -(yyy /. z -> k)

-k log(2/k^2)

trak = (yyy /. z -> (k - x)) + c

-k log(2/k^2) + k log((2 (k^2 - (k - x)^2)^(1/2))/(k^2 (k - x)) + 2/(k (k - x))) - (k^2 - (k - x)^2)^(1/2)

t1 = Plot[trak /. k -> 4, {x, 0, 4}, PlotRange -> {0, 10}, PlotStyle -> Farbig] ;

[Graphics:traktrix-b/traktrix_12.gif]

•Parameterdarstellung, t Steigungswinkel der Uhrkette

k - x == Cos[t] ; y ' == Tan[t]

•Mit (d y)/(d x) = (d y)/(d t) . (d t)/(d x) folgt

(d y)/(d t) == k Sin[t] Tan[t]
•Trennung der Variablen:

k ∫ Sin[t] Tan[t] d t

k (-log(cos(t/2) - sin(t/2)) + log(cos(t/2) + sin(t/2)) - sin(t))

y[t_] := k Log[(Cos[t/2] + Sin[t/2])/(Cos[t/2] - Sin[t/2])] - k Sin[t]

x[t_] := k (1 - Cos[t])
•Parameterdarstellung der Traktrix

t2 = ParametricPlot[{x[t], y[t]} /. k -> 4, {t, 0, 3}, PlotRange -> {0, 10}] ;

[Graphics:traktrix-b/traktrix_21.gif]

Show[t1, t2] (* es ist wirklich derselbe Graph *)

[Graphics:traktrix-b/traktrix_23.gif]

Converted by Mathematica  (May 16, 2004)


© Prof. Dr. Dörte Haftendorn
www.mathematik-verstehen.de
 [Kurven]  [Transzendente Kurven] 
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Apr 2004, update 16. August 2011 		Site-Info
Link zum Buch
www.leuphana.de/matheomnibus       www.doerte-haftendorn.de
http://haftendorn.uni-lueneburg.de     http://www.mathematik-sehen-und-verstehen.de