mathe.web-leuphana.de/algebra/algebra.htm
[Algebra] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik]
|
www.mathematik-verstehen.de |
| |
|
mathe.web-leuphana.de/algebra/algebra.htm
[Algebra] [Analysis [Cardano] [Geschichte] [MuPAD] [GeoGebra] [Didaktik] | |||
Algebraische Erweiterungskörper
Der Übergang von den rationalen 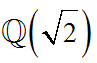 zu den algebraischen Erweiterungskörpern  u.a. gelingt wie die anderen algebraischen Zahlbereichserweiterungen
Schritt 1: Die Wurzel aus 2 ist keine rationale Zahl, d.h. sie lässt sich nicht als Bruch darstellen.  Schritt 2: 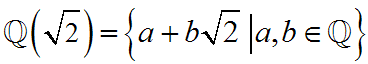 ist mit der üblichen Addition und Multiplikation ein Körper.
Dabei behandelt man die Wurzel(2) genau wie einen Term aus einem Variablennamen.
Dadurch gelten alle Gesetze, die in Q für das Rechnen mit Termen gelten.Die wirklich interessante Stelle ist, dass wider Erwarten das Inverse auch von dieser Gestalt ist. Die Klammern bei 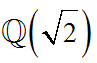müssen nicht unbedingt stehen.
Der Beweis ist beim Übergang von R nach C genau so.
|
