[Kurven] [Lehre] [Kegelschnitte] [Höhere Kurven] [Projekt Klasse 8 Johanneum] [Höhere Geometrie] [Probleme der Antike]
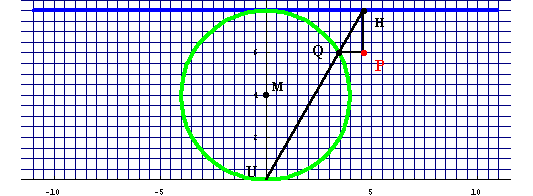 Konstruktion der
Versiera (Hexe).
Konstruktion der
Versiera (Hexe).Begründe, warum die Punkte B(8/4) und C(-8/4) gesicherte Punkte der Versiera sind und nenne einen weiteren gesicherten Punkt.
Die Gleichung dieser Versiera ist ![]() .
.
Bestätige, dass die drei sicheren Punkte die Gleichung erfüllen.
Berechne zu drei selbst gewählten x-Werten die zugehörigen y-Werte.
Zeichne die drei so gewonnenen Punkte oben farbig ein.
Mathilde hat im Lexikon als allgemeine Gleichung der Versiera gefunden: ![]() , welchen Wert hat a in dem obigen Fall?
, welchen Wert hat a in dem obigen Fall?
Mathix hat im Internet als allgemeine Gleichung der "Witch of Agnesi" gefunden: ![]() , welchen Wert hat r in dem obigen Fall?
, welchen Wert hat r in dem obigen Fall?
Begründe, warum beide Gleichungen dieselbe Kurve definieren. Was bedeuten a und r?
Mathinchen hat einige Versuche gemacht, die Gleichung umzuformen. Kläre durch Einsetzen eines sicheren Punktes, welche der folgenden Unformungsversuche sicher falsch sind.
a: ![]() b:
b: 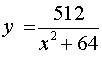 c:
c: ![]() d:
d:
Realisierung in Schritten im DGS Dynageo-Euklid
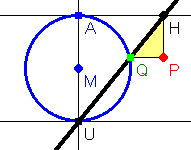 Erzeuge zuerst das rechtwinklige Kreuz bei U.
Erzeuge zuerst das rechtwinklige Kreuz bei U.
Du kannst das Koordinatenkreuz nehmen.
Setze M zugfest auf die Senkrechte. Konstruiere den Kreis mit dem Radius MU und erzeuge den Schnittpunkt A, errichte dort eine Senkrechte, also eine Parallele zur x-Achse.
Setze Q zugfest auf den Kreis, verbinde UQ mit einer Geraden, probiere ob alles zugfest ist.
Erzeuge mit dem Schnittpunkt-Werkzeug H und konstruiere mit zwei senkrechten Geraden den Punkt P.
Die Geraden sind hier versteckt.Ziehe an Q und beobachte P, vergleiche mit deiner Von-Hand-Konstruktion oben
.http://haftendorn.uni-lueneburg.de http://mathematik.uni-lueneburg.de |