Didaktik Leitseite URL
https://mathe.web.leuphana.de/didaktik/didaktik.htm
[Didaktik, Schule direkt] [Computer] [GeoGebra] [Funktionen und Graphen] [Analysis] © Prof. Dr. Dörte Haftendorn

Ein ganzer Sack voller neuer Möglichkeiten
Einstieg mit GeoGebra

Seite für die Mathematik-Lehrenden in Dachau, 26.9.05

Aktualisierte Seite zu GeoGebra
Zeichen-
erklärung		 Das ist das Applet, es ist gleich hier im Browser bedienbar, hat aber kaum weitere Möglichkeiten.
Das ist die GeoGebra-Datei selbst. Man klickt darauf und wählt öffnen.
Dann kann man sehen wie es gemacht ist und kann auch damit weitermachen. Das Eigene kann man auch bei sich speichern.
Erste Schritte
Einfache
Graphen		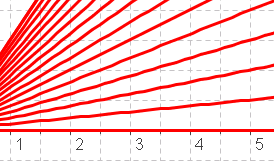 GeradenscharBauen Sie eine GeoGebra-Datei, bei der dieses Bild als Ausschnitt entstehen kann.
Tipps: Erst einen Parameter mit einem Wert eingeben, dann die Gleichung schreiben, dann mit "Objekt anzeigen" evt. einen Scheiberegler einfügen.
Übrigens kann man den Parameter mit den Pfeiltasten handwerkliche sicherer bedienen.
Lösung:
   
Erste Schritte
Kongruenz-
abbildungen		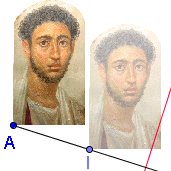 Doppelspiegelung Nehmen Sie diese Datei Abbildung-mit Bild und spiegeln Sie hintereinander an zwei Geraden
Welche Geamtabbildung ergibt sich jeweils?
Tipps: Speichen Sie Ihren ersten Fall unter eigenem Namen ab. Erzeugen Sie den Nächsten Fall mit "Umdefinieren".    
Erste Schritte
Gleichungen
  • Bauen Sie eine GeoGebra-Datei für den Schnitt zweier Geraden, bei der man die Geraden Parameter variieren und die Lösung ablesen kann.
    Lösung:
    Lineare Gleichung interaktiv visualieren, Lösung ablesen    download
  • Bauen Sie eine GeoGebra-Datei zum Lösen quadratischer Gleichungen durch den Schnitt von Normalparabel und Geraden, bei der man die Geraden-Parameter variieren und die Lösung ablesen kann.
    Lösung:
  • Quadratische Gleichungen mit der Normalparabel lösen       download
    		•
    Erste Schritte
    Analysis  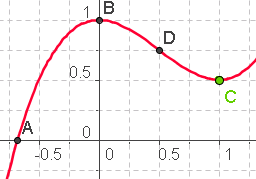  		 Kurvendiskussion
    Untersuchen Sie die Kurvenschar.
    Bestimmen Sie experimentell, welches die Kurve der Extrema ist.
    Welche Scharkurve berührt die x-Achse?
    Lösen diese Fragen auch analytisch und vergleichen Sie. Tipps: Setzten Sie vorher den Parameter k=1.
    Schreiben Sie dann den Funktionsterm.
    Verwenden Sie in in der Eingabezeile Nullestelle[f], Extremum[f], Wendepunkt[f].
    Machen Sie für das Extremum einen Haken bei "Spur an".
    Setzen Sie sich eine vermutete Funktion für den Bahn der Extrema mit einem neuen Parameter in des Bild und passen Sie dann gut an.
    Lösung:
       
    Erste Schritte
    Vektoren  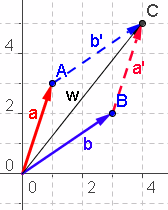  		 Vektorsumme
    Tipps: Vektoren befinden sich im Geraden-Menü. Umbenennen erreicht man mit der rechten Maustaste im Algebrafenster. Schreiben Sie a+b in der Eingabezeile, wenn a und b Vektoren sind.
    Lösung:
       
    Weiteres
    im elementaren
    Bereich
    Blättern Sie in dem Menu links nach Herzenslust. Für Einsteiger sind wichtig die über "Didaktik" und über "Funktionen und Graphen" erreichbaren GeoGebra-Seiten. Diese sind immer kenntlich an den blauen Symolen.
    Sehr Vieles ist auch bei "Geometrie" zu finden, dort allerdings sehr oft in Euklid-Dynageo ( Achtung nur mit IE surfen). Man kann aber alles leicht nach GeoGebra übertragen.
    Bei den "GeoGebra"-Seiten stehen schöäne Abstands-Probleme
    Freunde der Integrale werden auch fündig bei Stochastik, Verteilungen.
    Erkundung
    Analysis  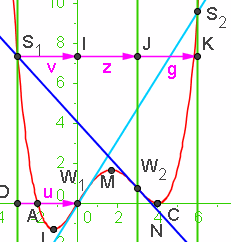  		 Polynome im Pantherkäfig
    Untersuchen Sie die Funktionen mit der Gleichung

    Setzen Sie die Parameter zuerst auf r=1, s=4, w=3.
    Erkunden Sie dann den Einfluss von r,s und w.
    Tipps: Verwenden Sie in in der Eingabezeile Nullestelle[f], Extremum[f], Wendepunkt[f]. und Tangente[W1,f]. Weiter brauchen Sie aus dem Menu das Schnittpunktwerkzeug, das bei "Punkt" untergebracht ist.
    Lösung:
       
    Weiteres dazu bei "Polynome im Affenkasten"
    Erkundung
    Analysis  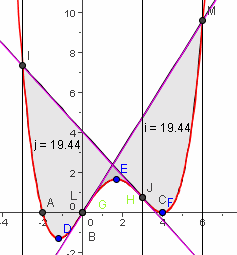  		 Pantherkäfig mit Flächen<br>Dieses ist ein Spezialfall der vorigen Funktion.
    Zeigen Sie, dass die beiden Flächen zwischen Wendetangente und Kurve links und rechts gleich groß sind.
    Tipps: Die Flächen erhalten Sie mit dem Befehl Intergal[g,f,o,x(S2], dabei muss g aber als Funktion neu geschrieben werden mit g(x)=f'(0) x    
    Lösung
     Aufgabe für GeoGebra zum Affenkasten der Polynome 3. Grades (pdf)
    Aufgabe zu Polynomtangenten (pdf)
    Lösungen im Bereich "Polynome im Affenkasten"
    [Didaktik, Schule direkt] [Computer] [GeoGebra] [Funktionen und Graphen] [Analysis]
    Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  März. 2005, update 14. August 2011
    Direkte Internetadressen
    [www.doerte-haftendorn.de]    [haftendorn.uni-lueneburg.de/mathe-lehramt]