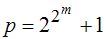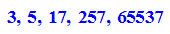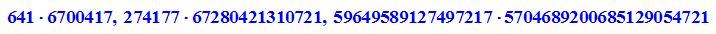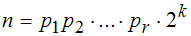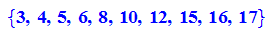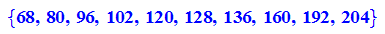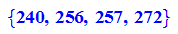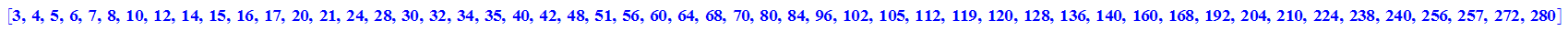Konstruierbare n-Ecke
und  Quasi-Konstruierbare n-Ecke
Quasi-Konstruierbare n-Ecke

Prof. Dr. Dörte Haftendorn: Mathematik mit MuPAD 3.1.1, Jan. 06 Update 31.01.06
Web: www.mathematik-verstehen.de haftendorn.uni-lueneburg.de/ing-math
Achtung: Menu ->Notebook->Evaluiere->Alle Eingaben
Prof. Dr. Dieter Riebesehl fand im Jan 06:
Das 7-Eck ist quasi-konstruierbar, d.h. mit Zirkel, Lineal und Parabellineal.
Der allgemeine Winkel ist drittelbar als Quasi-Konstruktion.
Damit ergibt sich eine Liste der quasi-konstruierbaren n-Ecke: n<300
Eine Fermat-Primzahl ist eine Primzahl der Gestalt 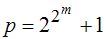
- fermatZahlen:=2^(2^m) +1 $ m=0..4
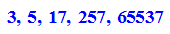
- factor(2^(2^m) +1) $ m=0..4
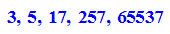
Diese ersten fünf Fermatschen Zahlen sind Primzahlen.
Die nächsten drei sind zerlegbar.
- factor(2^(2^m) +1) $ m=5..7
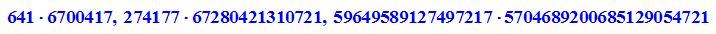
Bis heute hat man keine weiteren Fermatschen Primzahlen gefunden.
Satz von Gauß: Das n-Eck mit n>2 ist genau dann konstruierbar,
wenn n eine Zweierpotenz ist oder sich schreiben lässt als
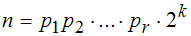
mit verschiedenen Fermat-Primzahlen pi
Gute Erklärungen und Ergänzungen in:
W. Henn: Elementare Algebra und Geometrie Vieweg 2003
ISBN 3-258-03201-4
Alle konstruierbaren n-Ecke bis n=300
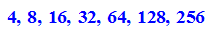

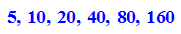
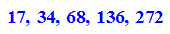

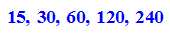
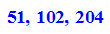
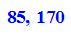
- dfs:=(3*5*17*2^k $ k=0..0)

- alle:=(z,d,f,s,h,df,ds,df):
- alle[1..10];alle[11..20];alle[21..30];alle[31..34];
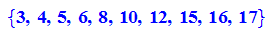

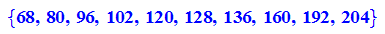
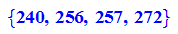
Dies sind die 34 für alle mit Zirkel und Lineal konstruierbaren n-Ecke, n<300
- matrix([sort([op(alle[1..17])]),sort([op(alle[18..34])])]);

Die nicht mit Zirkel und Lineal konstrierbaren n-Ecke sind: n<300
(gruppiert in nach Zehnern)
- (nk[k]:={}:
for i from 10*(k-1) to 10*k-1 do
if not contains(alle,i) then nk[k]:=(nk[k] union {i})
end_if
end_for ) $ k=1..30:
nk

######################################################
Quasi-konstruierbare n-Ecke
Dieter Riebesehl fand im Jan 06:
Das 7-Eck ist quasi-konstruierbar, d.h. mit Zirkel, Lineal und Parabellineal.
Der allgemeine Winkel ist drittelbar als Quasi-Konstruktion.
Damit ergibt sich eine Liste der quasi-konstruierbaren n-Ecke: n<300
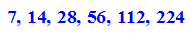
- alle7q:=(alle union map(alle,_mult,7))union {sq} //Menge, keine Doppelten
{3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 16, 17, 20, 21, 24, 28, 30, 32, 34,
35, 40, 42, 48, 51, 56, 60, 64, 68, 70, 80, 84, 96, 102, 105, 112,
119, 120, 128, 136, 140, 160, 168, 192, 204, 210, 224, 238, 240, 256,
257, 272, 280, 336, 357, 420, 448, 476, 560, 672, 714, 840, 896, 952,
1120, 1344, 1428, 1680, 1792, 1799, 1904}
- gr300:=[i $ i=300..2000]:
alle7qs:=sort(listlib::setDifference([op(alle7q)], gr300))
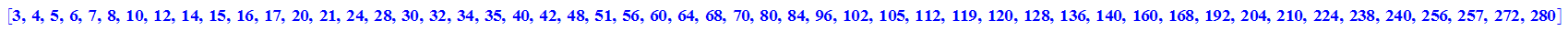
Jetzt ist dieses noch mit allen Dreierpotenzen zu multiplizieren.
- (li[k]:=map(alle7qs,_mult,3^(k-1))) $ k=1..5:
- alle73q:=(li[1].li[2].li[3].li[4].li[5]):
gr23000:=[i $ i=300..23000]:
alle73qk:=sort(listlib::setDifference(alle73q, gr23000));
nops(alle73qk);
[3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 17, 18, 20, 21, 24, 27, 28,
30, 32, 34, 35, 36, 40, 42, 45, 48, 51, 54, 56, 60, 63, 64, 68, 70,
72, 80, 81, 84, 90, 96, 102, 105, 108, 112, 119, 120, 126, 128, 135,
136, 140, 144, 153, 160, 162, 168, 180, 189, 192, 204, 210, 216, 224,
238, 240, 243, 252, 256, 257, 270, 272, 280, 288]

Hier stehen die streng- oder wenigstens quasi-konstruierbaren n-Ecke. n<300
Es sind 75 n-Ecke.
Übelegt man, dass nur die p-Ecke mit p prim Kandidaten für Quasi-Konstruierbarkeit sind, deren p-1 ausschließlich die Primfaktoren 2 und 3 hat, so könnten das 13-Eck und das 19-Eck quasi-konstruierbar sein.
Sie sind es tatsächlich: Beweis und neue Zählung der mindestens quasi-konstruierbaren n-Ecke bis n=300 Die noch nicht erfassten n-Ecke sind:
Die noch nicht erfassten n-Ecke sind:
Darunter könnten noch weitere quasi-konstruierbare n-Ecke sein.
Später werden wir hier ausführen, dass man die n-Ecke mindestens dann quasi-konstruieren kann, wenn n-1 nur die Primfaktioen 2 und 3 enthält.
Das führt zum 13-Eck, 19-Eck, 25-Eck,....
- (nkq[k]:={}:
for i from 10*(k-1) to 10*k-1 do
if not contains({op(alle73qk)},i) then nkq[k]:=(nkq[k] union {i})
end_if
end_for ) $ k=1..30:
nkq