www.mathematik-verstehen.de
Link zum Buch
[Knotentheorie] [Topologie] [GeoGebra] [Maxima]
| Definition: Eim Graph G besteht aus einer nichtleeren Menge E von "Ecken" und einer Menge K von "Kanten", wobei jede Kante zwei (nicht notwendig verschiedene) Ecken verbindet (mit zwei Ecken inzidiert).
"Schlingen" gehören nur zu einer Ecke. Zwei Ecken mit gemeinsamer Kante heißen "adjazent". Die Information über den Graphen kann z.B. durch eine "Adjazenzmatix", auch eine "Inzidenzmatrix" genannt, gegeben werden. Der "Grad einer Ecke" ist die Zahl von ihr abgehenden Kanten. Dabei werden Schlingen doppelt gezält. Zwei Graphen heißen "isomorph" wenn sie nach Umordnung dieselbe Adjazenzmatrix haben. Da es n! Umordnungen bei n Knoten gibt, ist der Nachweis von Isomorphie bei großen Graphen ein NP-schweres Problem. | ||||||
|
| ||||||
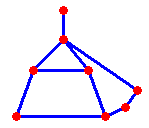 | Aufgabe zu Grundbegriffen
Lösung 1) Text Lösung 2) Text Lösung 3) Text Lösung 5) Text Lösung 6) Text |
|||||
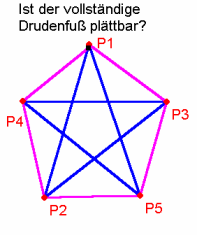
| Ein Graph heiß "planar" wenn er kreuzungsfrei gezeichnet werden kann. Man kann auch den Begriff "planar" spezieller für kreuzungsfrei gezeichnete Graphen verwenden und nennt dann die Graphen "plättbar", bei denen man die Kreuzungsfreiheit durch Umzeichnen erzwingen kann. | ||||||
 |
Aufgaben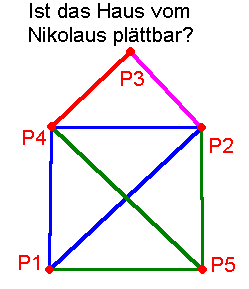 | Interaktionen | ||||
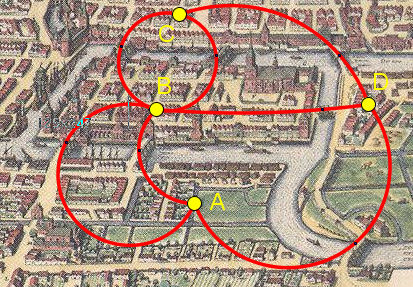 Euler und Graphen, Königsberger Brückenproblem Euler und Graphen, Königsberger BrückenproblemEin Kantenzug ist eine Folge von aneinanderstoßenden Kanten mit den zugehörigen Ecken. Ein Weg ist ein Kantenzug, bei dem keine Kante doppelt vorkommt. Ein Kreis ist ein geschlossener Weg. Ein eulerscher Weg ist ein Weg, der alle Kanten enthält. Der Graph ist dann "in einem Zug" zeichenbar. Ein eulerscher Kreis ist ein geschlossener eulerscher Weg. Er enthält also alle Kanten genau einmal und kehrt an seinen Anfangspunkt zurück.
| ||||||
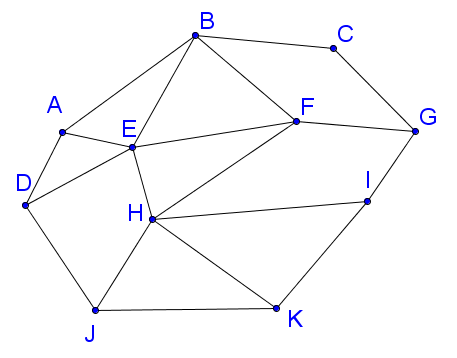 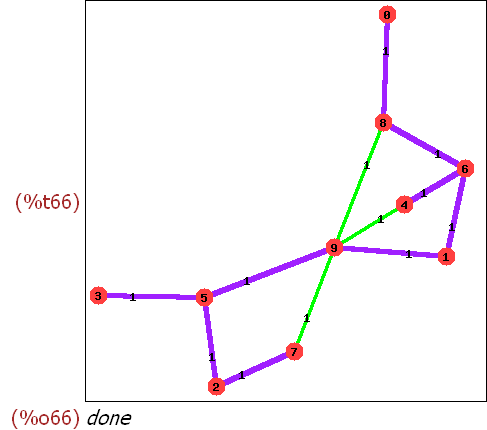 Ein Graph ohne Kreiswege heißt Baum. Ein Spannbaum ist ein Baum, der "den Graphen aufspannt", der also zusammenhängend ist und alle Knoten enthält. Ein Graph ohne Kreiswege heißt Baum. Ein Spannbaum ist ein Baum, der "den Graphen aufspannt", der also zusammenhängend ist und alle Knoten enthält.
Problem: Bestimme einen Spannbaum des Graphen:Einen Spannbaum kann man mit den Algorithmen "Breitensuche" oder "Tiefensuche" erreichen. Algorithmus "Breitensuche" Bei der "Breitensuche" geht man von einer Ecke aus alle Wege einen Schritt. Von allen neu erreichten Knoten geht man wieder auf allen abgehenden Kanten einen Schritt, betritt aber nie einen schon einmal betretenen Knoten. Das tut man, bis keine Knoten mehr übrig sind. Bei der "Tiefensuche" gräbt man sich immer weiter vorwärts durch den Graphen und merkt sich die Stellen, an denen man Alternativen hatte. Von diesen aus tut man das gleiche, stets ohne Kreise zu schließen, bis keine Knoten mehr übrig sind. Als Länge eines Weges (in eimem ungewichteten Graphen) wird die Zahl der in ihm enthaltenen Kanten genommen. Der Durchmesser eines Graphen ist der längste Weg ohne Kreise Die Taillenweite eines Graphen ist die Länge des kleinsten Kreises. Min. Delaunay-Triangulation, wikipedia Voronoi-Diagramm, Wikipedia | ||||||
| Bei "gewichteten Graphen" sind den Kanten Gewichte zugeordnet. Bei schlichten Graphen (d.h. ohne Doppelkanten) können diese auch in der Adjazenzmatrix angegeben werden. Nun wird als Weglänge die Summe der Kantengewichte genommen.
| ||||||
|
Eulerscher Polyedersatz
Ecken + Flächen = Kanten + 2 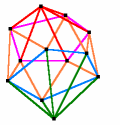
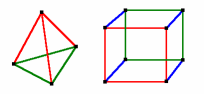 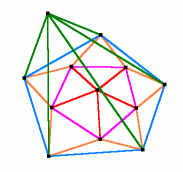 Kann man den Ikosaedergraph plätten? Kann man den Ikosaedergraph plätten? |
|||||
| Theorie der planaren Graphen | Wir betrachten planare, einfache (schlichte) Graphen, die zusammenhängend sind. (Zwei der Sätze beziehen sich auf n Zusammenhangskomponenten solcher Graphen.)
sind ausführlich aufeinander aufbauend bewiesen. e=Eckenzah, k=Kantenzahl, f=Flächenzahl, n=Zahl der Zusammenhangskomponenten |
|||||
| Deutschlandkarte Deutschlandgraph Übungsblatt Euklid-datei Österreichkarte
zugehörige interaktive Datei bei MatheVital, TUM (Richter-Gebert) | ||||||
| Klausur: Knoten, Graphen, Topologie | ||||||
| Gefunden im Internet | Graphentheorie aus Wikipedia | |||||
| http://www.natur-struktur.ch Bilder der Platonischen Körper und Abwicklungen
Eulerscher Polyedersatz mit ausführlichem Beweis Von den schweizer Lehrern Gregor Lüdi und Martin Lüscher |
||||||
| Reichhaltige Website Mathe Vital - Diskrete Mathematik von Prof. Dr. Richter-Gebert (München) und Prof. Dr. Ulrich Kortenkamp (Karlsruhe) | ||||||
www.mathematik-verstehen.de |
[Knotentheorie]
[Topologie]
[GeoGebra]
[maxima]
Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn |
Link zum Buch |
| www.leuphana.de/matheomnibus www.doerte-haftendorn.de http://haftendorn.uni-lueneburg.de http://www.mathematik-sehen-und-verstehen.de |