www.mathematik-verstehen.de © Prof. Dr. Dörte Haftendorn		Link zum Buch Site-Info
	http://haftendorn.uni-lueneburg.de/mathe-lehramt/knoten/knoten.htm [Graphentheorie]  [Topologie]    [GeoGebra]

Knotentheorie

Grundlagen	Grundknoten 1 (pdf) Erste Knotenfragen Lösungen dazu Seemannsknoten Knotengalerie Alle Primknoten bis Nr. 9.4 aus KnotPlot Knotentafel bis 9.36
	Definition und der Kleeblatt-Knoten Unknoten oder nicht? Weitere Knoten zum Üben Knoten zum identifizieren Reidemeister-Bewegungen Der Kretzschmar-Knoten aus der Vorlesung 07 Wie kommt man von K1 nach K4? Das Perko-Paar 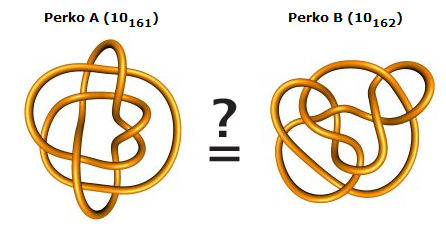mehr dazu http://knotplot.com/perko und Bilder mitKnotPlot Main, rechts oben Demo A obere Zeile "Perko"
Vortrag	"Diskret verknotet" Vortrag zu allen Teilen der Knotentheorie    Handzettel   download *.pptx "Diskret Verknotet" Vollständige Ausarbeitung (25 S) dieses Vortrags Darstellung einer Unterrichtseinheit zu Knotentheorie mit ausführlichen Beweisen
Färbbarkeit	Anwendung der Reidemeisterbewegungen beim Beweisen bei der "Färbbarkeit" 3-Färbbarkeit, Primknoten, zusammengesetzte Knoten, zum Drucken als , download als *.ppt 5-Färbbarkeit, p-Etikettierbareit, zum Drucken als , download als *.ppt Fünffärbbarkeit Färbbarkeit zusammengesetzter Knoten
Knoten p-Etikettierung und Alexanderpolynome mit Mathematica
Alexander- Polynome	Liste der Primknoten und ihrer Alexanderpolynome, mit Erklärung Alexanderpolynom Berechnung   Handzettel   im Webplayer     download Berechnung des Alexanderpolynoms eines Knotens         Alexanderpolynome für 8.18 und 8.16, vollstädige Berechnung
Zöpfe	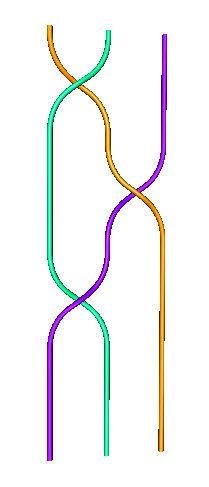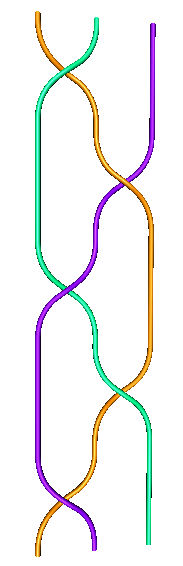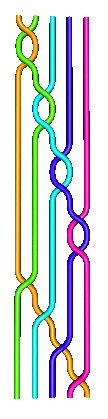Zopf aBa    Zopf aBaBA        Allerlei Zöpfe und Fragen     Lösungen dazu    AABBCCDDabcd Bilder mitKnotPlot gemacht: Zöfpe, engl. braid, mit Knotplot: main, rechts oben Demo A, dann 2. Zeile random braid. Es erscheint ein Zopf, bei dem man uberlegen kann, ob er beim Schießen ein Konoten wird oder eine Verschlingung. Dann kann man mit Klicken auf "close braid" die Wahrheit sehen. Wenn es zu klein wird: rechts auf main gehen und das scrollrad "scale" drehen. Selber Zöpe zeichnen: "Cons"-Reiter, unten "Braids" das Knotenwort eingeben. wenn es zu groß dargestellt ist, dann main scale-Rad drehen. (close hat hier leider nicht funktioniert)
Keltische Knoten Afrikanische Knoten und Verschlingungen
	Klausur: Knoten, Graphen, Topologie
Im Internet gefunden	http://www.knotplot.com Knotentheorie Knotplot-Site von Rob Scharein, Canada, englisch, mit Software sehr lohnend.
	Knotenzeichnungen zum Experimentieren Aus dem los-Alamos-Knoten-Projekt (s.u.)
	Grundlagen der Knotentheorie (pdf) Seminarvortrag, Niklas Peinecke, deutsch online: http://www.gdv.uni-hannover.de/~peinecke/aus.pdf Überarbeiteter Vortrag http://www.3d-meier.de/tut8/Seite302.html Linkliste zu Knoten und http://www.3d-meier.de/ Viel Interessantes Dies kam als Hinweis von Marc Häßler aus Köln, danke. http://www.inst.bnl.gov/~wei/contents.html The Knot Tutorial von Charilaos Aneziris http://www.javaview.de/services/index.html Dort auch Knoten
	Seminarankündigung Knotentheorie Uni Münster Direkte Adresse http://www.math.uni-muenster.de/math/inst/reine/inst/lueck/index.html
	Knoten-Seminarplan (Prof. Herrlich, / Schmithüsen) Uni Karlsruhe Direkt http://www.mathematik.uni-karlsruhe.de/~mi2/
	Projekt   Knotentheorie-Projekt aus Los Alamos, USA aus der Site Mega-Math für junge Schüler mit didaktischen Hinweisen (engl.) http://www.dctp.tv/#/mathematik-steckt-in-allen-dingen/schauenberg_gordische_knotenzoo von Birte Langhoff (leider kommt kurze werbung zuvor - nicht wundern)
	http://knotplot.com/

© Prof. Dr. Dörte Haftendorn www.mathematik-verstehen.de	[Analysis]  [Computer] Inhalt und Webbetreuung ©Prof. Dr. Dörte Haftendorn  Sept 2003, update 03. Mai 2012	Site-Info Link zum Buch
	www.leuphana.de/matheomnibus       www.doerte-haftendorn.de http://haftendorn.uni-lueneburg.de     http://www.mathematik-sehen-und-verstehen.de