haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/analysis.htm
haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/analysis.htm |
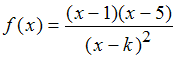 mit
mit 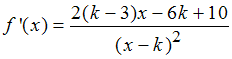
Nun wird f dazu gezeichnet.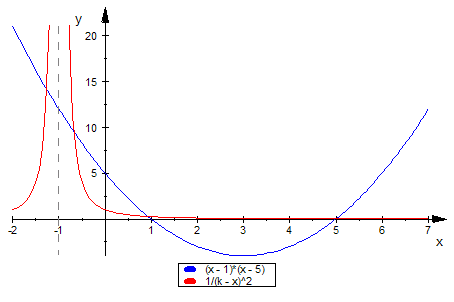

Bei diesem animierten Graphen zeigt sich,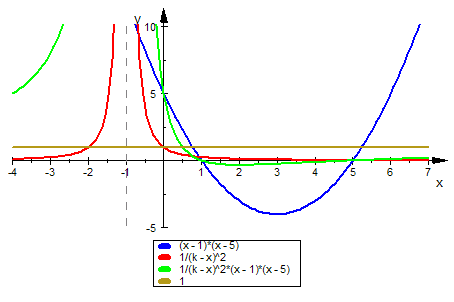

Das ist folgendendermaßen zu lesen: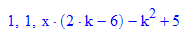
also: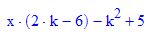
und das stimmt, weil im Zähler nur die Klammer aufgelöst ist.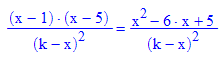
Also hat f für k=3 kein Extremum,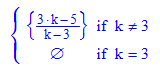
Wenn der Pol innerhalb von (1;5) steht, liegt das Extremum außerhalb.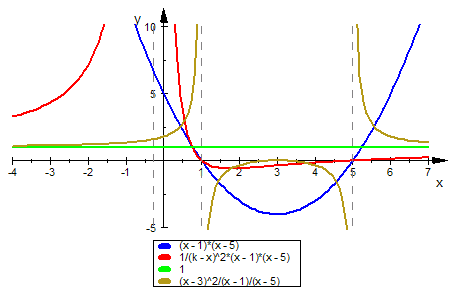

Interessanterweise ist die Kurve der Extrema die Kehrwert-Funktion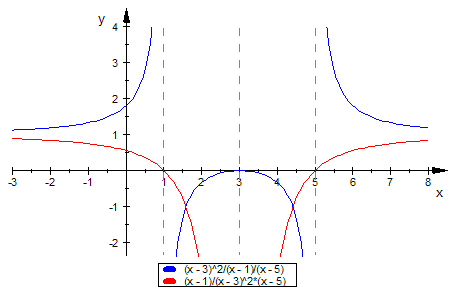

[haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math] |