haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/analysis.htm
haftendorn.uni-lueneburg.de/mathe-lehramt/analysis/analysis.htm |
Zu erwarten ist eine Parabel-Asymptote, da Zählergrad-Nennergrad=5-3=3-1=2 ist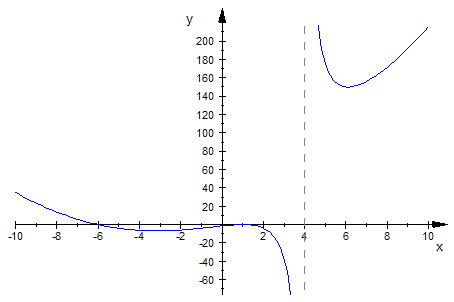

Der wahre "Rest" ist übrigens 90, denn: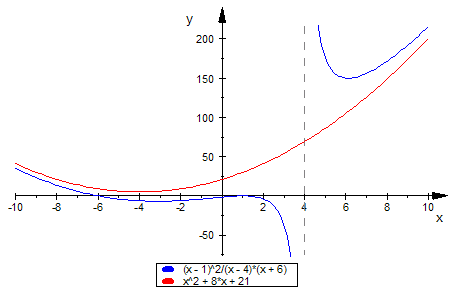

Probe, die stetige Fortsetzung als Parabel+Hyperbel
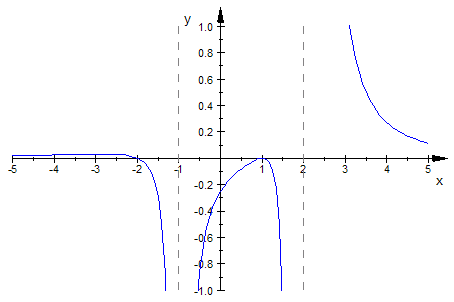
Links ist bei x= - 3 ist noch eine Nullstelle zu erwarten. (wegen (x+3)-Faktor).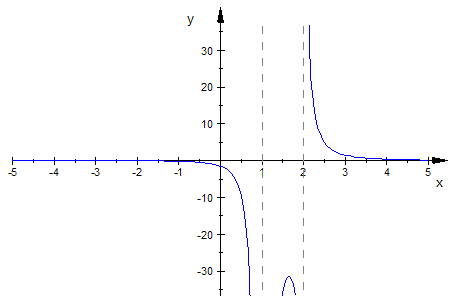

Definition Eine Polstelle x=a hat den Grad k, wenn im gekürzten Term der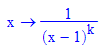
Fazit: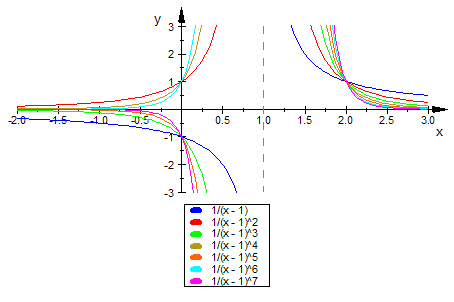

Also konnte man vorhersagen: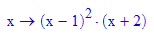
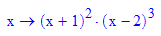

[haftendorn.uni-lueneburg.de/mathe-lehramt] [haftendorn.uni-lueneburg.de/ing-math] |