Sinus und Kosinus zum Wundern

Besonderheiten zur Stetigkeit und Differenzierbarkeit

Dazu noch eine stetig-differenzierbare Funktion, die eine relatives Minimum hat, bei dem das Vorzeichenwechselkriterium nicht erfüllt ist. Das Vorzeichenwechselkriterium ist i.A. nur hinreichend. Wenn man oszillierende Funktionen ausschlie&szlißt, ist das Vorzeichenwechselkriterium notwendig und hinreichend.

[Sinus] [Kosinus] [Werkzeuge] Beweise: [Differenzenquotient] [Ableitung] [Asymptoten] [Vorzeichenwechselkriterium]

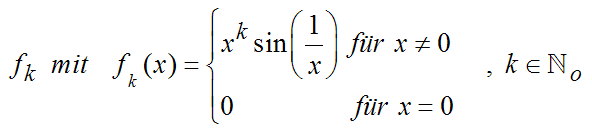k=0	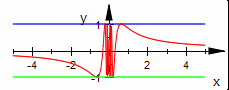Die Funktion ist unstetig an der Stelle x=0 und sonst stetig. Der Differenzenquotient hat keinen Grenzwert an der Stelle x=0. Die Ableitung hat eine Definitionslücke bei x=0. Die Steigung nimmt in jeder Umgebung von x=0 beliebig hohe Werte an. Interaktive Erkärung als Verkettung Gesamtbetrachtung
k=1	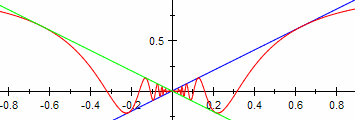Die Funktion ist überall stetig, auch an der Stelle x=0. Der Differenzenquotient hat keinen Grenzwert an der Stelle x=0. Die Funktion ist an der Stelle x=0 nicht differenzierbar, sonst aber überall. Die Steigung nimmt in jeder Umgebung von x=0 beliebig hohe Werte an. Die Ableitung hat eine Definitionslücke bei x=0.
k=2	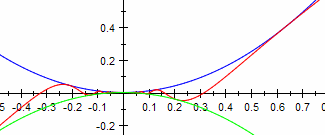Die Funktion ist überall stetig, auch an der Stelle x=0. Der Differenzenquotient hat den Grenzwert 0 an der Stelle x=0. Der Differentialquotient existiert überall, auch für x=0, dort hat er den Wert 0. Die Steigung nimmt in jeder kleinen Umgebung von x=0 jeden Wert zwischen -1 und 1 an. Die Funktion ist überall differenzierbar, aber nicht stetig-differenzierbar. Die Ableitung hat keine Definitionslücke bei x=0, ist aber dennoch nicht stetig.
k=3 k>3	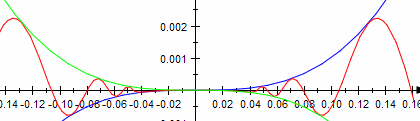Die Funktion ist überall stetig, auch an der Stelle x=0. Der Differenzenquotient hat den Grenzwert 0 an der Stelle x=0. Der Differentialquotient existiert überall, auch für x=0, dort hat er den Wert 0. Die Ableitung hat keine Definitionslücke bei x=0 und ist dort auch stetig. Die Steigung konvergiert für x gegen 0 ebefalls gegen 0. Die Funktion ist überall differenzierbar und sogar überall stetig-differenzierbar.
ggb	Alle weiteren Fälle in günstiger Darstellung
CAS	Erzeugung der Graphen in MuPAD Wundern mit Sinus(1/x) alle Fääle

[Sinus] [Kosinus] [Differenzenquotient] [Ableitung] [Asymptoten] [Vorzeichenwechselkriterium]

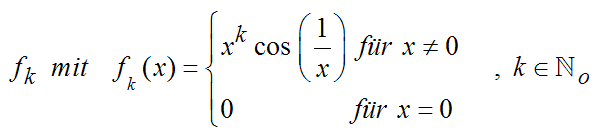k=0	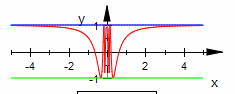Die Funktion ist unstetig an der Stelle x=0 und sonst stetig. Der Differenzenquotient hat keinen Grenzwert an der Stelle x=0. Die Ableitung hat eine Definitionslücke bei x=0. Die Steigung nimmt in jeder Umgebung von x=0 beliebig hohe Werte an. Interaktives Verständnis als Verkettung
k=1	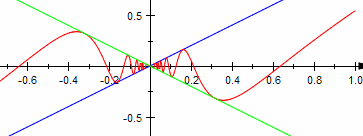Die Funktion ist überall stetig, auch an der Stelle x=0. Der Differenzenquotient hat keinen Grenzwert an der Stelle x=0. Die Funktion ist an der Stelle x=0 nicht differenzierbar, sonst aber überall. Die Steigung nimmt in jeder Umgebung von x=0 beliebig hohe Werte an. Die Ableitung hat eine Definitionslücke bei x=0.
k=2	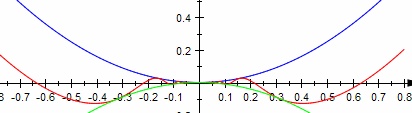Die Funktion ist überall stetig, auch an der Stelle x=0. Der Differenzenquotient hat den Grenzwert 0 an der Stelle x=0. Der Differentialquotient existiert überall, auch für x=0, dort hat er der Wert 0. Die Steigung nimmt in jeder kleinen Umgebung von x=0 jeden Wert zwischen -1 und 1 an. Die Funktion ist überall differenzierbar, aber nicht stetig-differenzierbar. Die Ableitung hat keine Definitionslücke bei x=0, ist aber dennoch nicht stetig.
k=3 k>3	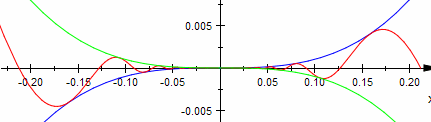Die Funktion ist überall stetig auch an der Stelle x=0. Der Differenzenquotient hat den Grenzwert 0 an der Stelle x=0. Der Differentialquotient existiert überall, auch für x=0, dort hat er den Wert 0. Die Ableitung hat keine Definitionslücke bei x=0 und ist dort auch stetig. Die Steigung konvergiert für x gegen 0 ebefalls gegen 0. Die Funktion ist überall differenzierbar und sogar überall stetig-differenzierbar.
ggb	Alle weiteren Fälle in günstiger Darstellung
CAS	Sinus-Wunderdinge mit Notes-Kommentaren Erzeugung der Graphen in MuPAD Wundern mit Cos(1/x)

Untersuchung des Differenzenquotienten an der Stelle x=0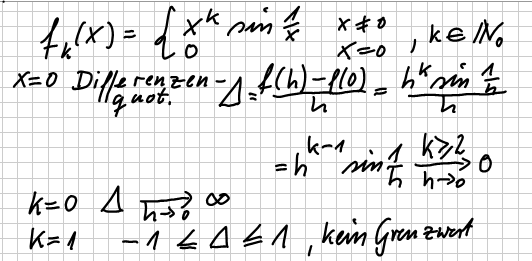
Ableitungen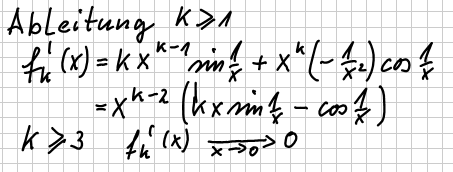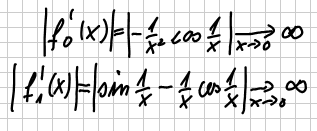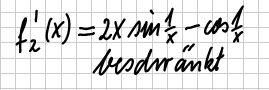
Asymptoten 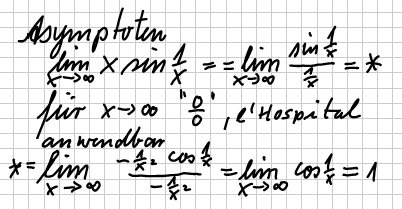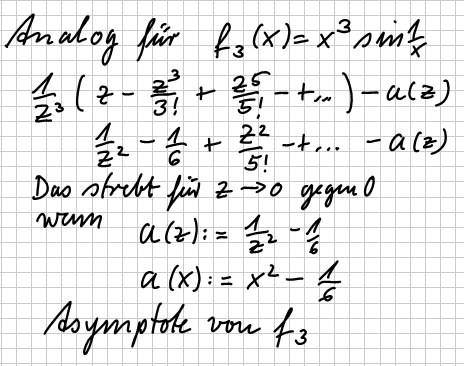Asymptoten interaktiv

Beispiel einer stetig-differenzierbaren Funktion, die eine relatives Minimum hat, bei dem das Vorzeichenwechselkriterium nicht erfüllt ist.
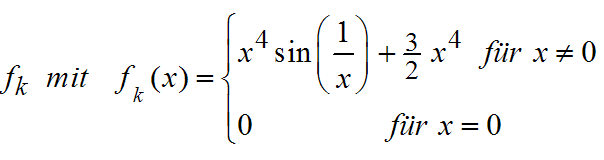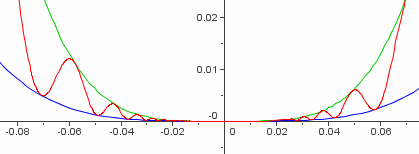Man sieht deutlich, dass es sich um eine relatives Minimum handet. Es ist die oben als stetig-digfferenzierbar nachgewiesene Funktion auf eine Potenzfkt 4. Grades aufgesetzt, daher ist auch diese Funktion stetig-differenzierbar. 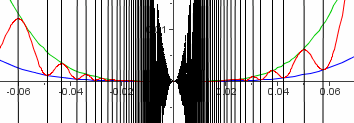Hier sieht man deutlich , dass die stetige Ableitung, die man nicht "durchzeichnen" kann, nicht für x<0 negativ und für x>0 positiv ist. Also ist trotz des Minimums das Vorzeichenwechselkriterium nicht erfüllt.
	Wer nix weiß sieht nix Hauptfall, Minimum ohne VZW, alle Fälle k=2-Fall
Bei Riemann	Weitere Zusammehänge, Nicht-Integrierbarkeit ....

[Differenzialrechnung] [Analysis] [Didaktik] [Computer] [Funktionen und Graphen] [Polynome] [Numerik] [MuPAD] [ing-math]

2005, update 16. August 2012

Direkte Internetadressen
[www.doerte-haftendorn.de] [haftendorn.uni-lueneburg.de/mathe-lehramt]