www.mathematik-verstehen.de	https://mathe.web.leuphana.de	© Prof. Dr. Dörte Haftendorn
https://mathe.web.leuphana.de/algebra/abbildungen/abbildungen.htm [Algebra] [Lineare Algebra] [Abbildungen] [Geometrie] [Computer]

Hauptachsen-Transformation
in analytischer Geometrie

Eigenwerte, Eigenvektoren	Eigenvektoren, Einführung Eigenvektoren Beispiel
Diagonalisierung	Diagonalisierung Diagonalisierungen in anderen mathematischen Gebieten
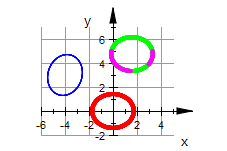
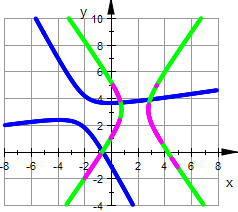
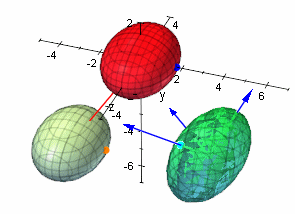
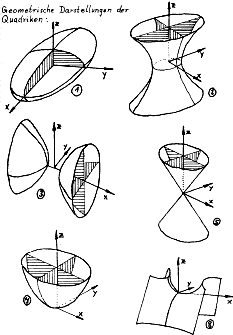
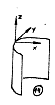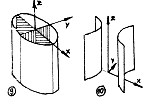
Kegelschnitte	Quadratische Formen mit x und y Rückwärtskonstruktion für Kegelschnitte in beliebiger Form und Lage Damit kann man viele schöne Beispiele erzeugen, die ganzzahlige Eigenwerte, selbst gewünschte schöne Eigenvektoren und einen selbst gewählten Mittelpunkt haben. Die folgenden Beispiele sind für die und zum Üben gemacht und meist auch damit erzeugt. Ellipse4 irgendwo 1 Ellipse 1 irgendwo Ellipse irgendwo 2, aber mit Drehspiegelung Hyperbel irgendwo Beispiel aus der Vorlesung Parabel irgendwo 1 Parabel irgendwo 2 Staatsexamensklausur mit Hautachsentransformation Löung, Ellipse [mehr zu Kegelschnitten]
Quadriken	Quadratische Formen mit x, y und z 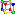Rückwärtskonstruktion für Quadriken in beliebiger Form und Lage & Damit kann man viele schöne Beispiele erzeugen, die ganzzahlige Eigenwerte, selbst gewünschte schöne Eigenvektoren und einen selbst gewählten Mittelpunkt haben. Die folgenden Beispiele sind damit auch meist erzeugt. Nr. 1: Ellipsoid Nr. 2: Einschaliges Hyperboloid [siehe Konstruktionsseite, unten] Nr. 3: Zweischaliges Hyperboloid [siehe Konstruktionsseite, unten] Nr. 5: Kegel [siehe Konstruktionsseite, unten] Nr. 7: Elliptisches Paraboloid Nr. 8: Hyperbolisches Paraboloid Nr. 9: Elliptischer Zylinder [siehe Konstruktionsseite, unten] Nr. 10: Hyperbolischer Zylinder Nr. 14: Parabolischer Zylinder [siehe Konstruktionsseite, unten] andere: Sonderformen, deren Darstellung nicht lohnt: Nr. 4:Nullteiliges Ellipsoid,kein reeller Punkt , Nr. 6: komplexer Kegel mit reeller Spitze , Nr. 11: nullteiliger Zylinder Nr. 12: zwei reelle Ebenen mit reeller Schnittgerade Nr. 13: konj- komlexe Ebenen mit reeller Schnittgerade Nr. 15: reelle, parallele Ebenen Nr. 16: reelle Doppelebene Nr. 17: komplexe Ebenen ohne reellen Schnittpunkt Damit sind alle Flächen 2. Ordnung erfasst. [mehr zu Rotationskörpern aus Kegelschnitten]
Die von Hand gezeichneten Bilder habe ich 1969/70 für ein Skriptum gezeichnet, das ich an der TU Clausthal für das Thema "Lineare Algebra" im Auftrag des Instituts erstellt habe. Es war etwa 15 Jahre lang in Gebrauch für Mathematiker, Naturwissenschaftler und von allem Ingenieure. Mein Student Thorsten Meyer hat das Ganze küzlich mühevoll eingescannt. Die 12 MB große Pdf-Datei können Sie sich herunterladen. Heutzutage habe ich in Büchern diese "Erkärungsbreite" nicht mehr gefunden. Gerade auch die Hauptachsentranstormation ist vollständig dargestellt. Download Haftendorn-Linalg-1970