Gebrochenrationale Funktionen

Definition:
Funktionen, die sich als Quotienten aus zwei Polynomen darstellen lassen, heißen gebrochenrationale Funktionen.

Mehr zu Polynomen Mehr zur Vielfachheit von Nullstellen

Einführung	Gebrochen-Rational, Grundlagen, Level 1 Beipiel mit Grundlegenden Erklärungen LEVEL 1 Dasselbe Beispiel in der Handschrift-Version (pdf)	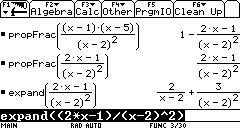Aus der Klausur (s.unten) mit TI voyage
Merksätze	Auch hier ist es sehr sinnvoll, den Graphen aus Bausteinen aufzubauen, indem man Zähler- und Nennerpolynom einzeln in dasselbe Koordinatensystem zeichnet. Zusammenhänge: Wo der Zähler 0 ist hat f Nullstellen, wenn der Nenner dort beschränkt und ungleich 0 ist. Wo der Nenner 0 ist hat f Polstellen,wenn der Zähler dort ungleich 0 ist. Wo der Nenner 1 ist, schneidet f den Zählergraphen. Wo der Zähler 1 ist, hat f den Kehrwert des Nennerwertes, wenn der Nenner dort ungleich 0 ist. Haben Zähler und Nenner gleichen Grad, gibt es eine waagerechte Asymptote. Ist der Nennergrad größer als der Zählergrad, ist die x-Achse Asymptote. Ist der Zählergrad größer als der Nennergrad, gibt es eine Polynom-Asymptote, deren Grad die Differenz aus Zählergrad und Nennergrad ist.
Interaktiv	Interessante interaktive Erkundung mit GeoGebra download
Lücken...	ungekürzter Term, stetige Fortsetzung, hebbare Unstetigkeit.... Beipiel mit Erklärungen LEVEL 2 Beipiel mit Erklärungen LEVEL 2
Aufwändigere Fälle	Gebrochen-Rational,Gemeinsame Nullstellen höherer Vielfachheit Level 3 Gemeinsame Nullstellen höherer Vielfachheit Pole mit und ohne Zeichenwechsel Level 3 Pole mit und ohne Zeichenwechsel Level 3<
Eine Grundkursklausur JG 13 zu dem Thema	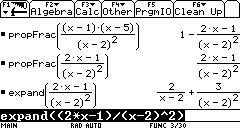alle drei Aufgaben Lösungen Aufgaben 1 und 2 Seite 1 Handschrift-Bild Lösungen Aufgaben 1 und 2 Seite 2 Handschrift-Bild Lösungen Aufgabe 3 Seite 1 Handschrift-Bild Lösungen Aufgabe 3 Seite 2 Handschrift-Bild Aufgabe 3 vollständig und erweitert untersucht mit MuPAD Download MuPAD 3 (oder 2)(Ziel Speichern unter....) Darin unten auch eine nette Forschungsfrage, die Lernende erkunden können. Dasselbe interaktiv mit GeoGebra download Die Zerlegung in Asymptotenterm und eigentlichen Bruch wird beim TI von propfrac geleistet. Die "Übersetzung": Partialbruchzerlegung ist falsch, die wird erst von expand(...) geleistet.
Weitere Aufgaben	Kleine systematische Betrachtung